Comparing Genomes
in terms of Protein Structure:
Surveys of a Finite Parts List
Mark Gerstein *
&
Hedi Hegyi
Department of Molecular Biophysics & Biochemistry
266 Whitney Avenue, Yale University
PO Box 208114, New Haven, CT 06520
(203) 432-6105, FAX (203) 432-5175
Mark.Gerstein@yale.edu
* Corresponding author.
Keywords: Databank Census, Protein Fold, Bioinformatics
Running Title: Comparing Genomes in terms of Protein Folds
Manuscript is 43 Pages in Length (including this one)
Graphics of Figures follow at end in sequence.
Version: f715
Submitted to: FEMS Microbiology Reviews
Abstract
We give an overview of the emerging field of structural genomics, describing how genomes can be compared in terms of protein structure. As the number of genes in a genome and the total number of protein folds are both quite limited, these comparisons take the form of surveys of a finite parts list, similar in respects to demographic censuses. Fold surveys have many similarities with other whole-genome characterizations, e.g. analyses of motifs or pathways. However, structure has a number of aspects that make it particularly suitable for comparing genomes, namely the way it allows for the precise definition of a basic protein module and the fact that it has a better defined relationship to sequence similarity than does protein function. An essential requirement for a structure survey is a library of folds, which groups the known structures into "fold families." This library can be built up automatically using a structure-comparison program, and we described how important objective statistical measures are for assessing similarities within the library and between the library and genome sequences. After building the library, one can use it to count the number of folds in genomes, expressing the results in the form of Venn diagrams and "top-10" statistics for shared and common folds. Depending on the counting methodology employed, these statistics can reflect different aspects of the genome, such as the amount of internal duplication or gene expression. Previous analyses have shown that the common folds shared between very different microorganisms - i.e. in different kingdoms - have a remarkably similar structure, being comprised of repeated strand-helix-strand super-secondary structure units. A major difficulty with this sort of "fold-counting" is that only a small subset of the structures in a complete genome are currently known and this subset is prone to sampling bias. One way of overcoming biases is through structure prediction, which can be applied uniformly and comprehensively to a whole genome. Various investigators have, in fact, already applied many of the existing techniques for predicting secondary structure and transmembrane (TM) helices to the recently sequenced genomes. The results have been consistent: Microbial genomes have similar fractions of strands and helices even though they have significantly different amino-acid composition. The fraction of membrane proteins with a given number of TM-helices falls off rapidly with more TM elements, approximately according to a Zipf Law. This latter finding indicates that there is no preference for the highly studied 7-TM proteins in microbial genomes. Continuously updated tables and further information pertinent to this review is available over the web at http://bioinfo.mbb.yale.edu/genome.
Introduction
The Sequencing of Complete Genomes Highlights the Finiteness of Molecular Biology
In the last three years a number of microbial genomes have been completely sequenced, generating tremendous interest, popular as well as scientific [1-3]. In particular, in 1995 the first genome of a free-living organism, the bacteria H. influenzae, was sequenced by Venter and colleagues, and two years later another landmark was reached with the publication of the yeast genome, a significantly more complex genome of a eukaryote [4, 5].
One of the most important points highlighted by having a complete genome sequence is the essential finiteness of molecular biology. That is, the complete sequence, while complex, describes all the parts necessary for microbial life.
A Structural Census, the Connection between Genomes and Structures
Simultaneous with all the progress being made in genomics, there is a tremendous investment
being made in structural biology. This is yielding great returns in the form of an exponentially increasing number of protein structures. All these structures fall into a very limited number of folding patterns, currently about 350 [6-10]. It is believed, furthermore, that we will eventually find that all naturally occurring protein structures are composed of very small number of folds, estimated to be ~1000 [11].The objective of this work is to discuss
various means of understanding this finite universe of genes in terms of an even more limited repertoire of protein folds. This is the subject of the new field of structural genomics [12, 13]. One can achieve some form of understanding by performing large-scale surveys, looking at the occurrence of protein structures and various protein structural features in the genomes of different organisms. We use the term "structural censuses" to describe these surveys, emphasizing the intent to provide a comprehensive accounting.To do such a structu
ral census properly, one needs to cluster together 3D structures into a library of folds and then to match up genome sequences to structures in this library. One also needs a way to characterize the sequences without structural homologues in rough structural terms. This is usually done via various prediction techniques, such as those for secondary structure or transmembrane helices. Then one does "fold counting," enumerating how often a fold or structural feature occurs in a given genome or organism. These specific aspects of a structure census will be discussed at length. But before doing so it is worthwhile to provide some perspective on the general questions addressed and how this work relates to other types of genomic analysis.The Overall Question: At What Structural Resolution Do Organisms Differ?
One interesting question addressed by a census of structures is to what degree certain folds occur only in certain branches of the "evolutionary tree." To put it in somewhat extreme terms, can one explain the obvious morphological differences between two microorganisms (e.g. between yeast and E. coli) in terms of their having different protein folds? Alternatively, it may be that most folds occur in every organism in the same way that the genetic code and many basic biochemical pathways (such as glycolysis) are almost universally shared. Currently, it is only possible to answer this question anecdotally, in terms of individual structures. One can find evidence for either viewpoint. On one hand, the immunoglobulin fold, which is usually closely associated with the eukaryotes (e.g. in the vertebrate immune system), has been found in bacteria, where it carries out a very different function [14]. On the other hand, the small DNA-binding fold known as the zinc finger so far appears to be confined to eukaryotes [15].
This question can be rephrased as, "At what structural resolution do organisms differ?" Structurally, microorganisms appear different on the micron scale, as they have different internal cell structures, but on the scale of single Ångstroms they appear nearly the same, containing similar proportions of C, H, O, N, P, and S atoms (Fig. 1). At what structural resolution can one start seeing differences? It is probably not at the level of secondary structure (~10 Å) since all organisms are composed of essentially similar proportions of alpha helices and beta sheets (see below). Is it at the level of protein super-secondary structure (e.g. four-helix bundles or beta-alpha-beta units) or at the level of whole domain folds? Or perhaps it is at a higher level, involving the large-scale organization and regulation of essentially identical protein parts.
This question is especially interesting when one considers the diverse physical environments inhabited by these organisms -- from high temperature and pressure for Methanococcus, to normal temperature and pressure for yeast, to high acid for Helicobacter.
A Structural Census as a Particular Type of "Occurrence Analysis" in Genomics
Analyzing the occurrence or frequency of folds in genomes is a particular example of a general type of comparative genomics we dub "occurrence analysis." This involves comparing how often a particular entity (e.g. a sequence motif) occurs in various genomes, and seeing what fraction of a collection of entities occurs in one genome as compared to another. Several different types of occurrence analysis have been previously performed, studying genomes at many different levels.
Starting from the most basic units, genomes have been compared in terms of the relative frequencies of short oligonucleotide and oligopeptide "words" [16-19].
On the level of individual genes or proteins, the degree of gene duplication in a number of genomes has been ascertained [20-25]. Other works have investigated the occurrence of conserved families in several different genomes [26-30]. This can be performed on a large-scale in a highly automated fashion [31-36]. The recent growth of databases makes such automatic and objective systems highly desirable. In particular, with the data of many complete genomes now available, the often arbitrary functional assignment of homologous genes can be replaced with a system of orthologs and paralogs (genes with a common ancestor, separated by speciation and presumably performing the same function, versus genes generated by duplication within the same organism). A semi-automatic approach was recently developed that compared several genomes and derived clusters of orthologous groups (COGS) [28]. The approach is straightforward: If one knows all the potential candidates in a genome for a certain protein function, one can pick the best one based on the best match to a protein of known function. If the best matches occur consistently among the same group of proteins from several distantly related genomes, the proteins are classified as COGS.
An important application of single-gene occurrence analysis is "differential genomics." When two closely related genome sequences are compared, the difference,
i.e. those genes that are present only in one of them, may give a clue to the unique nature of the microbe in question. For example, a comparison between E. coli and H. influenzae revealed 116 genes that are present only in the latter [37]. Differential genomics may have useful applications for attacking microbe-related diseases [38, 39], e.g. finding genes unique to pathogenic organisms can help in developing antibiotics against them.Occurrence analysis can also be carried out on the level of whole metabolic pathways and systems [40-42]. This work has yielded many interesting conclusions in terms of
the pathways that are modified or absent in certain organisms. For instance, many of the respiratory enzymes in E. coli are missing in H. influenzae, and the metabolism in the latter seems to be biased to a relatively nitrogen-rich and anaerobic environment [4, 43, 44].Why Analysis of Structure is Particularly Advantageous for Genome Comparison
The analysis of structure is expected to be particularly advantageous for genome comparison for two reasons.
Structural Modules are Precisely Defined and Relatively Few in Number
First, structure allows one to define a protein module (or shared part) in both a more precise and more general sense.
It is possible (and quite productive) to define modules purely in terms of conserved "blocks" in sequence alignments or small, but distinctive, "motifs" shared by many related proteins [45-58]. However, functioning protein modules fundamentally consist of units of 3D structure. In fact, it is usually believed that these structural units form physically interacting "folding domains," and attempts have been made to see how well they correspond to exon boundaries and other linear sequence features [59-61]. This is often not a simple relationship as many structural modules are discontinuous in terms of sequence -- as when a polypeptide chain starts in one domain, goes through a hinge region into a second domain, and then returns to the first domain. Nevertheless, relating modules defined on the sequence level to structure enables them to be better characterized. This is especially true for groups of aligned structures, which allow the definition of a conserved structural core [62, 63].
Also, one expects analysis of structure to reveal more about distant evolutionary relationships than sequence comparison, since structure is more conserved than sequence or function [64, 65]. In other words, it is at the level of protein structure where the biologists sees the fewest "parts" and greatest amount of redundancy and reuse.
Similarity in Sequence is More Closely Related to Similarity in Structure than in Function
A second reason that structural analysis is useful for genome comparisons is that the relationship between sequence similarity and structural similarity is much better defined than the corresponding relationship between sequence and function.
It is generally accepted that proteins with similar sequences usually have similar structures. A decade ago Lesk & Chothia systematically investigated the relationship between divergence in sequence and that in structure [64, 66]. Using the limited amount of data available at the time (32 pairs of homologous structures among 25 proteins), they found that the extent of the structural changes is directly related to the extent of the sequence changes. As shown in figure 2, we have repeated the calculations here using a much larger data set. (Details of the calculations are described in the legend.) Expressing sequence similarity in terms of the more modern statistical terminology (i.e. P-value instead of percentage identity), we find very similar results to the original work of Lesk & Chothia. There are, of course, exceptions where similarity in sequence does not imply similarity in structure. These usually occur for small proteins, e.g. an artificially designed sequence of a four-helix bundle could be made more than 50% identical to a predominantly beta-sheet protein [67, 68].
The relationship between sequence similarity and functional similarity is much less clear [69]. In part, this is because it is much more difficult to precisely specify a function than a sequence or a structure. Moreover, even in cases where the functional identification is well specified, there are several examples where highly similar sequences have completely different functions - i.e. same fold but different function. A well-known example is the structural protein eye-lens crystallin and the metabolic enzyme gluthatione S-transferase [70], which have sequence and structural similarity but differ in function. An extreme example is provided by the enzymes lactate dehydrogenase and malate dehydrogenase. In protein engineering experiments, Wilks et al. managed to convert one into the other by changing only a single amino acid [71].
The opposite situation can also be observed, namely when the same function is performed by several proteins unrelated in structure and sequence - i.e. same function but different fold. A good example is chloroperoxidase, which has an alpha/beta fold in the prokaryote Pseudomonas but has an all-alpha fold in fungi [72, 73]. There are many more examples of this type of convergent evolution in enzymes [74].
Elements of a Structural Census: Construction of a Fold Library
Thus far, we have described how comparing genomes in terms of structures is a particular form of "occurrence analysis" and how structure provides a particularly advantageous subject for comparison. Now we outline what goes into a structure census, its methodological "elements," and discuss some conclusions from recent work. An essential element in a survey of known structures is the construction of a library of folds. This is expected to be an essential data structure in molecular biology, organizing the collection of gene families like the columns in the chemical periodic table [75].
Pairwise Structural Comparison and Alignment: Automatic vs Manual
To build a fold library, one must have a way of comparing and aligning protein structures (see figure 3). One approach is to do this manually, the approach taken for the scop classification of protein structures [7]. On another extreme, there are a number of algorithms for automatically comparing structures and clustering them into fold families [76-89]. Finally, there is a hybrid approach, based on both automatic and manual comparison [10, 90].
Completely automatic methods have the advantage of speed and objectivity. However, the fold classifications produced by a computer are not always as understandable or reliable as those produced by humans. Furthermore, although manual classification is slow, if it is done correctly, it only has to be done once.
Various Automatic Methods for Structural Comparison
To get a perspective on the automatic methods, it is useful to compare structural alignment with the much more thoroughly studied methods for sequence alignment [91, 92]. Both methods produce an alignment, which can be described as an ordered set of equivalent pairs (i,j) associating residue i in protein A with residue j in protein B. Both methods allow gaps in these alignments which correspond to non-sequential i (or j) values in consecutive pairs — i.e. one has pairs like (10,20) and (11, 22). And both methods reach an alignment by optimizing a function that scores well for good matches and badly for gaps. The major difference between the methods is that the optimization used for sequence alignment is globally convergent whereas that used for structural alignment is not. This is the case for sequence alignment because the optimum match for one part of a sequence is not affected by the match for any other part. Structural alignment fails to converge globally because the possible matches for different segments are tightly coupled, as they are part of the same rigid 3D structure.
This lack-of-convergence has led to a large number of different approaches to structural alignment, the methods differing in how they attack the problem. No current algorithm works all of the time (i.e. for all the pathological cases). The methods also differ in the function they optimize (the equivalent of the amino acid substitution matrix used in sequence alignment) and how they treat gaps. Some of the methods effectively compare the respective distance matrices of each structure, trying to minimize the difference in intra-atomic distances for selected aligned substructures [80, 83, 93]. Other approaches, in contrast, directly try to minimize the inter-atomic distances between two structures, using repeated application of dynamic programming [77, 89, 90, 94, 95]. This allows structures to be aligned in a similar fashion to normal sequence alignment [96]. A similar approach is taken in minimizing the "soap-bubble area" between two structures [87]. Other methods involve other techniques, such as geometric hashing or lattice fitting [79, 85, 86].
Fusing a Multiple Alignment into a Structural Template
The classification of the entire databank using a variety of the automatic and manual procedures outlined above has recently been undertaken by a number of groups [7, 83, 97-101], resulting in the scop, FSSP, LPFC, CATH, and HOMALDB databases. These databases group the known structures into ~350 fold families, some of which are quite large (e.g. currently the PDB contains over 166 antibody structures). Because of the great numbers of structures and of families, it is worthwhile to summarize the common features within a family, whilst separating out the variable ones. That is, one wants to know which regions are conserved and which are highly variable, and to fuse all the conserved regions into a single "core structure" template (figure 3). A number of approaches have been developed to tackle this problem through determining a mean and variance for an ensemble of multiply aligned structures and then picking the low variance atoms as "core" [8, 62, 102, 103].
Searching the Genome with Structural Templates
Clustering the Structure Databank into Sequence Templates
Once a library of folds has been constructed, one wants to build sequence templates based on it and then use these to search the genome. A necessary methodological preliminary is clustering the known structures into a number of (sequence) representative domains, using a variety of single or multiple linkage approaches [6, 67, 104-106]. Currently, the PDB can be clustered in ~1200 representative domains. Then using structure comparison, one finds that these representatives are distributed amongst 338 folds, giving about three sequence families per fold [6]. The fact that the number of folds is so much less than the number of sequence families highlights the fact that many of the evolutionary similarities between highly diverged organisms may only be apparent in terms of structure [107]. Folds can, in turn, be ranked the number of different families of non-homologous sequences they are associated with. Folds uniting many distinct sequence families have been dubbed superfolds [108]. These may represent intrinsically stable and favorable structural arrangements, as suggested by a variety of analyses [108-110].
At this point one has ~350 3D-structural alignments, each of which "connects" a number of non-homologous sequences. These can be used as "seeds" to build up large sequence alignments from the major databases using standard pairwise searching tools - e.g. the popular BLAST and FASTA programs
on the SwissProt and GenBank databases [111-115]. A number of recently developed methods of transitive sequence matching (through a third intermediate sequence) are expected to improve the sensitivity of these pairwise searches somewhat [116-119].As many of these alignments contain quite a few sequences, it can be advantageous to fuse them into a consensus pattern or template, just as is done with structures [62] (Fig. 3). For this, a variety of probabilistic approaches
can be used. A most popular representations is the Hidden Markov Model (HMM) [120-125]. This is a generalization of the sequence profile, and like a profile it gives an explicit probability for each of the 20 amino acids to occur at each position in the model [126]. The HMM goes beyond a profile in associating with each position an explicit probability for introducing a gap (either for insertion or deletion).Microbial Genome Sequences
Once formed, sequence templates can be compared directly against the genomes. This can take place in a variety of ways. The most straightforward is to just compare each sequence in the template against the genome using the standard pairwise comparison programs (e.g. FASTA, BLAST, or straight Smith-Waterman [111-113, 127]). Alternately, one can use profile or HMM searching programs for those sequences that are part of an explicit pattern. However, in doing this one has to consider some important issues related to bias (see below).
At the time of this writing there are 13 microbial genome sequences currently available (Table 1). These already provide a most diverse comparison -- representing microbes from the three kingdoms of life (Eukarya, Eubacteria, Archea), from different environments (room temperature and pressure to high temperature and pressure, and neutral pH to highly acidic), with a wide range of genome sizes (0.6 to 13 Mb), and with a variety of modes of life (from parasite to autotroph).
One point worth mentioning is that the genome data is constantly changing and is contingent on the current "state of the art" in gene finding. The data used in any analysis reflects a particular snapshot of this ongoing process. For instance, the current E. coli data file is version M52, containing 4290 ORFs. This is a more recent version and contains a different number of ORFs than the one referred to in the official publication (M49, containing 4288 ORFs) [128]. For yeast there is some uncertainty regarding whether all of the ORFs in the web site file are really genes. In particular, 5888 of the 6218 ORFs are definitely believed to be genes, but there is some question about the remaining 330 [129]. Furthermore, quite a number of yeast sequences (initially) annotated to be ORFs are, in fact, transposons, which should properly be segregated from the rest of the proteome [130].
Similarity in Both Sequence and Structure is Best Described Statistically
Similarities are best expressed statistically in terms of a P-value
The preceding section was concerned with comparison, both for structure and sequence. To do this right, one needs to be able to assess the significance of a given comparison score – i.e. what does a score of 392 mean? This is often quite subtle and, in a sense, relates to the fundamental problem of what constitutes similarity in biology. Moreover, it is a most important issue with respect to large-scale genome surveys, which involve hundreds of thousands of comparisons. It is essential to have a rapid and automatic method to assess the significance of a given comparison score (i.e. to set a threshold), as it is neither possible nor desirable to do this by hand.
The best way to assess significance is to see how a particular similarity score compares in a statistical sense to all the others.
A major development in the past few years has been the implementation of probabilistic scoring schemes for doing just this [131-137]. These give the significance of a match in terms of a P-value rather than an absolute, "raw" score (such as percent identity or RMS). A P-value is the chance that one would get a given similarity score (or better) from a random alignment. That is, P(s > S) = .01 means that a randomly generated score s would be greater than the threshold score S (e.g. 392) 1% of the time. The P-value gives the rank of a score relative to all the other possible scores. It places scores from very different programs in a common framework and provides an obvious way to set a significance cutoff (i.e. at P < 0.0001 or 0.01%).P-values are closely related to another quantity called the e-value, which is the number of false positives expected with a given score threshold in a whole databank comparison. Thus, the e-value is just the databank size multiplied by the P-value.
Determination of P-values involves determining the score distribution for true negatives, i.e. for
random alignments. This can be done in a number of ways: simulating random alignments, analytically deriving the score distribution for a random alignment, or doing an all-vs-all comparison of the databank and curve-fitting to the observed score distribution.Statistics for Sequence Similarity
For sequences, P-values were first used in the BLAST family of sequence searching programs, where they are derived from an analytic model for the chance of an arbitrary ungapped alignment [131, 135]. P-values have subsequently been implemented in other programs such as FASTA and gapped BLAST using a somewhat different formalism [116, 136-138]. In all the formalisms, P-values for sequence comparison are derived from an extreme value distribution. That is, sequence comparison scores are observed to follow a distribution like exp(-S-exp(-S)), which has a much longer "tail" than the rapidly falling off normal distribution exp(-S2). Such a distribution arises naturally from repeatedly considering the maximum of a number of independent, random variables. This is in contrast to the normal distribution, which arises from repeatedly considering sums of random variables.
In general, P-values give similar results to more conventional scores, such as percent identity, but they have been shown to be better calibrated and more sensitive for marginal similarities, taking into account compositional biases of the databank and the query sequence [94, 132, 133]. In particular, Brenner et al. tested the applicability of probabilistic scores to the detection of structural relationships [67, 139, 140]. They found that the FASTA e-value closely tracked the error rate against a test set of known structural relationships. That is, with regard to the number of false positives, expectation tracked reality.
Statistics for Structural Similarity
Some of the current methods for structural alignment have associated with them probabilistic scoring schemes. In particular, one method computes a P-value for an alignment based on measuring how many secondary structure elements are aligned, as compared to the chance of aligning this many elements randomly (VAST) [86]. Another method expresses the significance of an alignment in terms of the number of standard deviations it scores above the mean alignment score in an all-vs-all comparison (i.e., a Z-score) [8, 83].
We have recently developed a simple empirical approach for calculating the significance of a structural alignment score based on doing an all-vs-all comparison of the databank and then curve fitting to the observed score distribution for the true negatives [90, 94]. We can apply our approach consistently to both sequences and structures. For sequences, we compared our fit-based P-values with the differently derived statistical scores from commonly used programs such as BLAST and FASTA and found substantial agreement. For structure alignment, we follow a parallel route to derive an expression for the P-value of a given alignment in terms of a structural alignment score.
We find that scores from structure alignment follow a similar extreme-value distribution to those in sequence comparison, allowing one to adopt a uniform statistical formalism for both comparison techniques. (As dynamic programming applied to either sequence or structure alignment essentially finds a maximum score over many possible alignments, it is quite reasonable that this should be the case. However, this is not trivially obvious, as the dynamic programming score does not result from considering the maximum of truly independent variables.)
A nice aspect of structural alignment is that one can visualize exactly what is meant by a strong similarity in comparison to a marginal one. Examples shown in figure 4, which shows a strong similarity (for two globins), a weaker one (for two immunoglobulins), and a very marginal one.
Overall "Inventory" Statistics in a Census Calculation
Distribution of Folds Amongst Genomes (Venn Diagrams)
After setting a uniform comparison threshold and running the fold library against the genomes, it is possible to see how the known folds are distributed amongst different genomes, or partial genomes. There are a number of web sites that compile this data automatically – e.g. PEDANT and GeneQuiz [33, 141]. However, few detailed analyses have been published, mostly because only recently have enough complete genomes become available for this sort of comparative analysis.
A recent work illustrates what is initially possible [24]. This analysis focussed on three of the first genomes to be sequenced, the first ones from each of the major kingdoms: i.e., H. influenzae (a eubacteria, [4]), M. jannaschii (an archaeon, [142]), and S. cerevisiae (yeast, a eukaryote [129]).
As shown in Figure 5, the analysis can be conceptualized in terms of a Venn diagram, similar to those used for studying the occurrence of motifs and sequence families [143, 144]. About half of the known folds (148) are contained in at least one of the three genomes, and 45 folds are shared amongst all three genomes. These shared folds presumably represent an ancient set of molecular parts.
It is possible to classify each fold as all-alpha
, all-beta, alpha/beta, alpha+beta, or "other" using the original definitions of Levitt & Chothia and then to see how the folds corresponding to each structural class are distributed among the genomes [145, 146]. Overall, the genomes contain a disproportionate number of mixed folds (a/b and a+b, 83/148), and the shared fold are even more enriched in a/b super-secondary structures, with 38 of 45 having a mixed architecture.A related analysis looked at the occurrence of folds in different groups of organisms (e.g. plants vs. animals) [147]. This did not involve complete genomes but rather partitioning the sequence databank into a number of distinct phylogenetic sets. Such an analysis suffers from various biases (as discussed below), but it is nevertheless suggestive, showing that more closely related organisms had a greater number of folds in common.
It is expected that many more analyses such as these will be undertaken in the future as more genomes are sequenced and structures determined [148]. It is difficult to express the shared folds amongst more than three genomes in terms of a Venn diagram, so other representations become useful, such as cluster trees [149].
Frequency that Folds Occur in a Genome ("Top-10 lists")
Another simple statistic to look at is how often a particular known fold occurs in a genome, i.e. the fold frequency. In the previous work comparing three genomes, these frequencies were expressed in terms of "top-10" lists for the most common folds in a genome [24]. As was the case for the folds overall, most of the common folds have an a/b architecture.
Combining the frequent fold analysis with the Venn diagram, one can determine the common folds that are shared by all genomes. As shown in figure 6, ordered in terms of their frequency of occurrence, the top-five common and shared folds when comparing yeast, Haemophilus influenzae, and Methanococcus jannaschii are the P-loop containing NTP hydrolase fold, the Rossmann fold, the TIM-barrel fold, the flavodoxin fold, and the Thiamin-binding fold. Each of these folds is associated with basic metabolism (as opposed to other functions such as transcription or regulation). They are all classic a/b proteins and share a remarkably similar super-secondary structure architecture, with a central sheet of parallel strands with helices packed onto at least one face of this sheet. Moreover, the topology of the central sheet is very similar in all the proteins. Almost all of the connections are right-handed links between adjacent parallel strands through an intervening helix packed onto the central sheet.
These top-10 lists rank folds by how often they occur in the genome, tending to emphasize highly duplicated genes. Folds can also be ranked by a number of other criteria. For instance, they can be ranked by the number of non-homologous sequence families they are associated with, i.e. their superfold ranking. This number is not always correlated with how often the fold occurs in microbial genomes, but it is the case that superfolds are among the most common folds found in genomes. Folds can also be ranked in terms of expression level, essentially a ranking by mRNA occurrence in the cell. This has already been done in non-structural terms for all the genes in yeast [150-152]. In table 2, we see how this expression level ranking maps onto folds. Using data from DeRisi et al. [152], the figure shows the most highly expressed folds in yeast grown in two different conditions (high sugar and low sugar, aerobic vs. anaerobic conditions). The ranking of folds is clearly different from that purely based on duplication.
The Problem of Sampling Bias Affects the Statistics
General Issue of Bias in the Databanks
One of the most important issues in doing a large-scale survey is avoiding biases. Because of the preferences of investigators, some types of sequences or structures are over-represented and others are under-represented in the databanks. For instance, in GenBank there is an over-representation of globins from humans relative to flies. Moreover, a particular fold may be found in the human but not in the fly simply because not all the fly sequences are currently known. Focussing only on organisms for which complete genomes are known eliminates this obvious form of bias. However, there is another bias that is not overcome by knowledge of complete genomes. The selection of proteins in the PDB is also biased by the preferences of individual investigators and by the physical constraints on what will crystallize (or can be studied by NMR spectroscopy). For instance, the PDB currently contains about 5500 entries (5493 identifiers and 10781 domains). This total includes 222 structures for T4 lysozyme, but only a single structure for the "equally important" tyrosine kinase and topisomerase-II proteins.
Structures in the PDB are also biased towards certain commonly studied organisms. Thus, a much larger percentage of folds is known for the bacteria Haemophilus in comparison to the archeon Methanococcus, even though both have roughly the same number of genes [24].
Another issue related to the state of the structure databank is that the absolute counts found in a given genome survey are contingent on the evolving contents of the databank. Thus, over time as more structures are added to the databank, one should expect such statistics as the most common folds and number of shared folds to change somewhat.
The Multi-domain Nature of Proteins Creates Counting Problems
A second type of bias has to do with the fact that protein structure is fundamentally arranged around the level of folding domains whereas statistics for genomes are often calculated and best understood in terms of the number of genes (Fig. 7). For instance, when one talks about how prevalent the kinase and Rossmann folds are in the yeast and E. coli genomes, one is implicitly comparing the number of matches that known kinase and Rossmann fold structures have in the ~6200 yeast ORFs relative to the ~4300 E. coli ORFs. However, it is possible for a single gene to contain a number of kinase fold domains or to simultaneously contain both a kinase and Rossmann fold. Thus, the total number of domains in a genome is probably a better standard for these comparisons. Unfortunately, one does not know this number. But one does know that the number of domains is not related simply to the number of genes. For instance, on average a protein is about 50% larger in yeast than in E. coli (317 vs. 466), meaning that there are probably twice as many possible domains in yeast as in E.coli.
Another problem emanating from the multi-domain nature of proteins is highlighted in Figure 7. When clustering genes based on their sequence similarities, simple single-linkage clustering can give potentially misleading results. As has been pointed out before, it may group together two multi-domain proteins (AB and bc) containing the two unrelated domain folds (A and c) based on their having similarity only through a common domain (B and b) [42, 50].
Subtle Biases in Comparison Techniques
A final, rather subtle form of bias results from the type of sequence comparison method used. Different pairwise comparison methods (e.g. Smith-Waterman vs. FASTA) and different thresholds will give rise to different absolute numbers of fold counts, but the relative values between different folds will usually remain comparable. However, as discussed above, there are other, potentially more sensitive, methods of comparing sequences to structures – e.g. profiles, HMMs, and motif analysis, and threading [55, 125, 153-155]. These latter methods find more homologues for certain folds, particularly those for which multiple alignments are available. However, the sensitivity improvement is not consistent for all folds. This is not advantageous for a large-scale survey where uniform sampling and treatment of the data is more important than sensitivity. One is more concerned with accurate relative numbers than with absolute values. Cobbling together a survey through a disparate collection of tools and patterns creates the problem of devising consistent scores and thresholds. This problem is particularly acute in the case of manually derived sequence patterns and motifs, since an expert on a particular fold or motif would expect his pattern to find relatively more homologues than a pattern not so expertly constructed. The simple approach of just using pairwise comparison, applying the same objective procedure to each fold, circumvents these problems somewhat. Furthermore, it has an added advantage in that it can be performed automatically without manual intervention and, consequently, can easily be scaled up to deal with large data sets.
Various weighting, sampling and clustering schemes attempt to correct for both obvious and more subtle biases [156-160]. Potentially, even methods developed to correct for biases in governmental censuses may be of use [161, 162]. However, in a large-scale structure survey nothing can really make up for essential folds that are missing.
When will we know all structures in a genome?
One way to overcome the biases in the databank is to wait until we know all structures, or at least all the structures in a number of genomes. How long will this take? We tried to answer this question in a rough fashion by doing the "back of the envelope" calculation shown in figure 8. We looked at how the fraction of structurally "uncharacterized" genome sequence is decreasing each year, as more structures are determined. By uncharacterized sequence we mean, regions of genome sequence that are not matched by a known fold or annotated to be a transmembrane helix or low-complexity region. (Our exact definition is given in the legend to the figure.) For the purposes of this calculation, one imagines that the genomes were sequenced in 1975. Then, based on the number of folds known in that year the fraction of uncharacterized region is computed. The same thing is done for 1976, 1977, and so on. Finally, based on the values for all genomes over the last ten years, a trendline is extrapolated to zero uncharacterized regions. This gives the rather pessimistic conclusion that all the structures will not be known until 2050.
Our conclusion is a bit more conservative than other estimates [6, 11, 163], which estimate that all the structures in certain small genomes could be known in a decade. This is due to a number of reasons:
(1) The statistics here are in terms of residues rather than whole sequences. This helps correct for the "multi-domain" counting problem discussed above.
(2) The trendline is based on the average of eight known genomes, rather than focusing on the smallest one, M. genitalium, which Fischer & Eisenberg [163] analyzed.
(3) Only standard sequence comparison rather than more sensitive threading techniques were used to match sequences with structures. Fischer & Eisenberg, for instance, reported a 6% improvement in sensitivity over standard sequence comparison when using their threading technique.
(4) The method of estimating folds here does not correct the duplications that may exist in the uncharacterized sequence – that is, unknown folds that occur multiple times. These may reduce the number of future structure determinations necessary to match all the genome sequences. However, our calculation also does not correct for duplications in the characterized regions – that is, for known folds that occur multiple times. Thus, we hope that by ignoring duplication altogether it will "cancel-out" somewhat. However, if unknown folds were significantly more duplicated than known ones this would tend to inflate the time necessary to determine all the folds.
Prediction for Characterizing Sequences without a Structural Homologue: Methods
Basic Single-Sequence Secondary Structure Prediction
A
conservative calculation, thus, shows that it will take a while before we can truly compare microbial genomes in terms of known folds. Consequently, to compare genomes, today, comprehensively in terms of protein structure, we will need to use structure prediction. As compared to counting known folds, structure prediction has both advantages and disadvantages when applied to genome comparison. On the plus side, it does not suffer from the problem of biases that so plagues the fold counting, since it can potentially be applied uniformly to all the ORFs in a genome. However, the downside is that structure prediction is inaccurate, to varying degrees (whereas fold counting can be made almost perfectly "accurate" with suitably severe sequence comparison thresholds).Although the basic hypothesis that the amino-acid sequence completely specifies the 3D structure of a protein is believed to be valid, no current "ab initio" method has proven successful in predicting 3D structure from the sequence alone [164-166]. Consequently, by structure prediction we mean more limited, one-dimensional, predictions for secondary structure, which assign individual residues in the protein sequence to discrete states likestrand, coil, or helix (soluble or transmembrane).
One of the most straightforward secondary structure prediction methods is the GOR method [167-169]. This is a well-established and commonly used approach. It is statistically based so that the prediction for a particular residue to be in a given state (say Ala in a helix) is directly based on the frequency that this residue occurs in this state in a database of solved structures (taking into account neighbors at ±1, ±2, and so forth). For the most up-to-date version of the program, the prediction for residue i is based on a window from i-8 to i+8 around i, and within this window, the 17 individual residue frequencies (singlets) are combined with the frequencies of all 136 possible di-residue pairs (doublets) [167].
Multiple-Sequence Secondary Structure Prediction, Improved Accuracy but Some Pitfalls
The GOR method has a well-documented single-sequence prediction accuracy of 65%. This is considerably lower than the current "state-of-the-art" methods that incorporate multiple sequence information. In particular, Rost & Sander used a two-layered neural network trained on a non-redundant database of 130 protein chains to predict the secondary structure [170]. If they include protein family information in the form of multiple-sequence alignments, they get an overall three-state accuracy of 71%. Salamov & Solovyev’s nearest-neighbor algorithms give slightly better results (three-state accuracy to 72.2%) [171]. The DSC method (Discrimination of Secondary structure Class), which is very similar in conception to GOR but uses multiple sequences, achieves 70.1% accuracy [172]. Finally, the method of Livingstone & Barton [173] groups residues based on the similarities and differences in their physicochemical properties, achieving a similar accuracy.
The conspicuous agreement in accuracy among the multiple-alignment methods (~70%) may be related to a baseline level of agreement between the secondary structure of two proteins both having the same 3D fold [174]. Note, however, that using multiple alignment methods comprehensively on genomes introduces subtle biases into the analysis. One only gets higher accuracy where one can construct a multiple alignment. However, it is not possible to obtain multiple sequence alignments for most of the proteins in a genome. Consequently, bulk predictions of all the proteins in a genome based on multiple-alignment approaches are in a sense skewed. One gets two distinctly different types of prediction, depending on how many homologues a given protein has.
Transmembrane-Helix Prediction
Several prediction methods have been developed for transmembrane helices. Some of them are based on parameters derived from the intrinsic properties of amino acids, usually their oil-water transfer energies. A widely used example is the GES hydrophobicity scale [175]. To use this, one calculates the hydrophobic character of each 20-residue sequence span (the typical length of a transmembrane helix) using the values in the scale and compares them against a cutoff (usually -1 kcal/mol◊residue). A value under this cutoff is taken to indicate the existence of a transmembrane helix. Similar approaches were taken by other authors, who used different scales, e.g. the Kyte-Doolittle or the Eisenberg scales [92, 176-179].
Other transmembrane-prediction methods involve accumulating statistics on the small set of known membrane proteins in the databanks, calculating "propensity" values for each position in the sequence or using neural networks [180-182]. Both these approaches utilize multiple-alignment information to improve accuracy [180, 182]. Furthermore, by analyzing compositional differences between the membrane-spanning segments, they can predict not only the location, but also the orientation of the helices, based on the observation that positively charged residues are more abundant on cytoplasmic side of the membrane [178-180, 183].
There is a subtle problem that exists in databank-derived membrane protein structure potentials. Since there are so few known membrane protein structures, each of them rather strongly affects the potentials. Moreover, many of the sequences characterized as "gold-standard" membrane proteins were in fact determined to be such by their original depositors through the application of computer programs, not by experiment. These then are often carelessly used as training data later. Thus, one has prediction serving as data, again biasing the potentials to find more of what we already know. This problem even exists in regard to membrane proteins characterized by experiment, as even in this case the exact boundary of the TM helix is often determined through application of computer programs.
Prediction for Characterizing Sequences without a Structural Homologue: Results
When applied in bulk to the currently known genomes, secondary structure prediction has shown that many microbial genomes have remarkably similar composition of helices and strands (by residue, 40% helix and 17% strand, and by element, half-and-half) (Table 3) [24, 184]. Furthermore, the occurrence of all-alpha, all-beta and mixed architectures appears also to be very similar [185]. This result is rather surprising when one considers that the genomes have significantly different amino acid composition and different amino acids have different physical propensities to confer secondary structure [24]. There are, however, some differences in the occurrence of super-secondary structure elements.
There have also been many surveys of the occurrence of membrane proteins in genomes [24, 39, 149, 164, 182, 186-190, 191 ]. The overall number of membrane proteins found depends somewhat on the prediction method and threshold used. Nevertheless, there seems to be a broad agreement that ~20-30% of the proteins in microbial genomes are membrane proteins, with yeast having a slightly larger fraction. Membrane protein structures can be classified by how many transmembrane (TM) helices they have. In all the surveys, the number of TM-helices per protein follows a similar decreasing pattern in each genome, with fewer proteins having large numbers of TM-helices.
To summarize this data, one can plot the fraction of proteins with a given number of TM-helices on a log-log scale and get a straight line trend as shown in Figure 9 [149]. The fraction F of proteins in the genome with a given number n of TM-helices can be fit with the expression F(n) = .18 n-1.8, where n ranges from 0 to 15. (Without great degradation of the fit, the even simpler expression 1/[5n2] can be used as well.) This expression has a form like that of the Zipf’s Law that often occurs in the analysis of word frequency in documents [192]. Similar Zipf-law-like expressions have been found to apply in a variety of other situations relating to the occurrence of proteins (e.g. in relation to the occurrence of oligopeptide words [193-195]). Moreover, this particular functional form for the occurrence of proteins with a given number of TM-helices falls off smoothly with increasing numbers of helices. This implies that there is no particular preference (i.e. local maximum) for proteins with seven TM-helices and, thus, suggests that this heavily studied group of proteins, which includes G-protein coupled receptors, is not exceptionally prevalent in microbial genomes.
Most of the membrane-protein surveys agree on this absence of 7-TM proteins in microbial genomes; some also claim to find more 6 and 12 TM proteins in bacterial genomes corresponding to well known families of transporter proteins [24, 187, 189, 191]. In contrast, surveys of the incomplete (and highly biased) set of human sequences and the unfinished worm genome find a relative abundance of 7-TM proteins in these multi-cellular organisms [187, 191].
Discussion and Conclusion
Summary
We have described how genomes can be compared in terms of protein structure. As the number of genes in a genome and the total number of folds in nature are both quite limited, these comparisons take the form of surveys, which we dub censuses, of finite parts lists. Surveys of the occurrence of protein folds in genomes have many similarities with other types of whole-genome "occurrence" analyses, focussing, say on motifs or pathways. However, structure has a number of special aspects that make it particularly advantageous for genome comparison. It has a more certain relation to sequence similarity than does function, and it allows for precise definition of module, or basic unit. An essential element for a structure census is a library of protein folds that arranges all the known structures into "fold families." We described how this library could be built up by using an automatic comparison program. We show how important statistics are for defining the similarities within this library and between templates in the library and genome sequences. After building the library one can count folds in genomes, expressing the results in the form of Venn diagrams and "top-10" statistics for shared and common folds. Previous analyses have shown that folds shared between very different microorganisms - i.e. between those in three different kingdoms - have a remarkably similar structure, being comprised of repeated beta-alpha-beta super-secondary-structure units. A major problem with this sort of analysis and fold counting in general is that only a small subset of the folds in a complete genome are currently known and this subset is prone to various forms of sampling bias. One way of overcoming biases is through structure prediction, which can be applied comprehensively to all ORFs in a genome. There are many variants on the principal prediction techniques for secondary structure and transmembrane-helices (TM-helices). These have been applied in a comparative sense to a number of genomes by various investigators, giving similar results: that the fraction strands and helices in a number of genomes is approximately constant and that the fraction of proteins with a given number of TM-helices falls off with more TM elements approximately according to Zipf law. This latter result indicates that there is no preference for the highly studied 7-TM proteins in microbial genomes.
Continuously updated tables and further information pertinent to this review is available over the web at http://bioinfo.mbb.yale.edu/genome.
General Perspective on the Scale of a Genome Survey
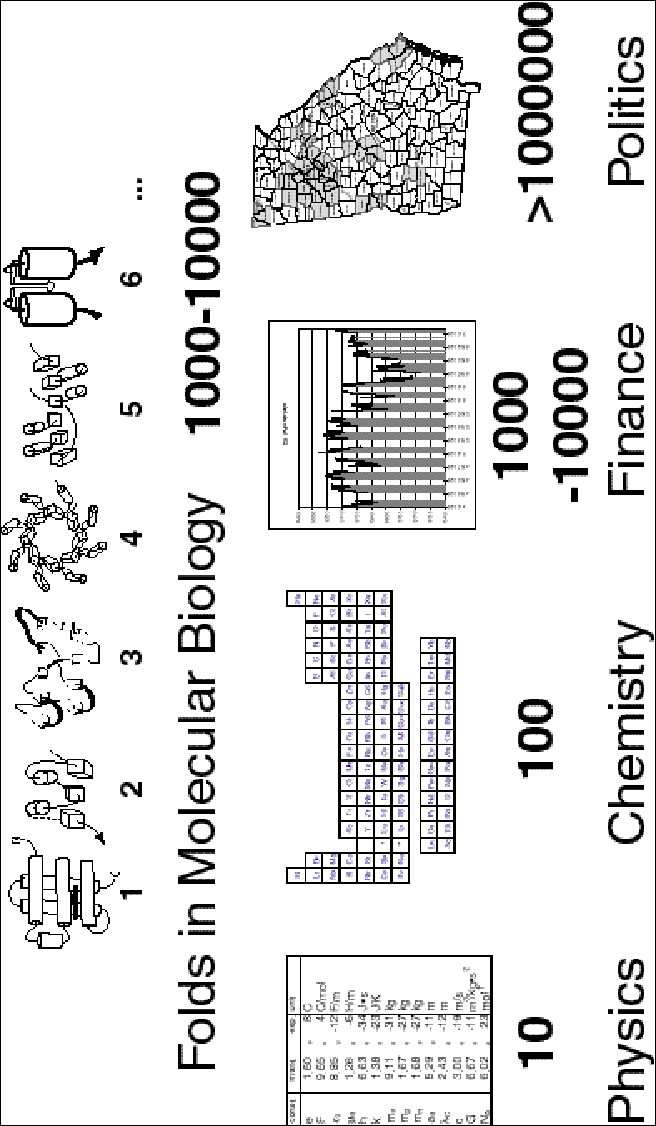
As a concluding point, it is worthwhile to put the scale of the genome surveys into a broader context. As described above, it is believed that there are roughly 1000 folds (i.e. fundamental objects) in nature. These can be arranged into a fold library, and when completed this fold library will constitute a most important "data structure" in molecular biology. How does it compare with the fundamental data structures in other scientific disciplines? As shown in figure 10,, in physics there are ~10 basic data objects, the fundamental constants, the speed of light, the mass of an electron, etc. This is a small enough number so that one can keep them all in memory. Physicists understand the world through constructing intricate mathematical relationships between these constants and actual physical observables. In chemistry, there are about an order of magnitude more fundamental data objects, the 113 chemical elements. This is too many things to keep in one's head at once so usually these elements are written down on a page in the form of the periodic table. Chemists understand the world by seeing trends and periods in this table. In (molecular) biology we expect to have at least an order of magnitude more data objects in the fold library than the elements in the periodic table. Moreover, each fold represents a substantially more complex entity than a physical constant or chemical element. Consequently, it is not possible to keep the fold library in one's head or write it down on a piece of paper. It has to be stored in a computer database. What type of understanding can we expect from this database, which we can carry with us in our minds? It is not going to be mathematical relationships as in physics; rather, it is going to be statistics, in the sense of the top-10 fold list and the P-value for similarities, discussed earlier. Thus, our goal in these large-scale surveys is really statistical understanding.
It also interesting to note that the data-set scale in molecular biology is approximately the same as that faced by economists and financiers studying the stock market. The stock market contains roughly 1000-10,000 well-defined objects, i.e. public companies. While it is, of course, possible to study these each individually, it is not possible to do this for all companies simultaneously, and economists understand the stock market through various key statistics, summarizing large groups of companies (e.g. market indices for various sectors). The next larger size data set occurs in other branches of social sciences, such as demographics and political science, when one is concerned with surveys of whole populations, as in political polls. Here the number of fundamental data objects can easily exceed 1 million. However, the exact number and description and of each data object is no longer possible, even in the context of a computer database, so one is no longer surveying a finite list, but rather sampling a large population to estimate various statistics.
Acknowledgements
We thank Cyrus Wilson for help in preparing figure 2. MG acknowledges the ONR for support (Grant N00014-97-1-0725).
References
1. Nowak, R (1995) Bacterial Genome Sequence Bagged. Science 269, 468-470.
2. Langreth, R (1997) Scientists Unlock Sequence Of Ulcer Bacterium's Genes. Wall Street Journal B1.
3. Wade, N (1997). Thinking Small Paying Off Big In Gene Quest. New York Times, 3 February 1997, A1 (front page).
4. Fleischmann, R D, et al. (1995) Whole-genome random sequencing and assembly of haemophilus influenzae rd. Science (Washington D C) 269, 496-512.
5. Goffeau, A & names], e a (1997) The Yeast Genome Directory. Nature 387(Supp), 5-105.
6. Brenner, S E, Chothia, C & Hubbard, T J (1997) Population statistics of protein structures: lessons from structural classifications [In Process Citation]. Curr Opin Struct Biol 7, 369-376.
7. Murzin, A, Brenner, S E, Hubbard, T & Chothia, C (1995) SCOP: A Structural Classification of Proteins for the Investigation of Sequences and Structures. J. Mol. Biol. 247, 536-540.
8. Holm, L & Sander, C (1996) Mapping the Protein Universe. Science 273, 595-602.
9. Holm, L & Sander, C (1997) New structure -- novel fold? Structure 5, 165-171.
10. Orengo, C A, Michie, A D, Jones, S, Jones, D T, Swindells, M B & Thornton, J M (1997) CATH--a hierarchic classification of protein domain structures. Structure 5, 1093-1108.
11. Chothia, C (1992) Proteins — 1000 families for the molecular biologist. Nature 357, 543-544.
12. Shapiro, L & Lima, C D (1998) The Argonne Structural Genomics Workshop: Lamaze class for the birth of a new science. Structure 6, 265-267.
13. Pennisi, E (1998) Taking a structured approach to understanding proteins [news]. Science 279, 978-979.
14. Holmgren, A & Branden, C I (1989) Crystal structure of chaperone protein PapD reveals an immunoglobulin fold [see comments]. Nature 342, 248-251.
15. Berg, J M & Shi, Y (1996) The Galvanization of Biology: A Growing Appreciation for the Roles of Zinc. Science 217, 1081-1085.
16. Blaisdell, B E, Campbell, A M & Karlin, S (1996) Similarities and dissimilarities of phage genomes. Proceedings of the National Academy of Sciences of the United States of America 93, 5854-5859.
17. Karlin, S & Burge, C (1995) Dinucleotide relative abundance extremes: a genomic signature. [Review]. Trends in Genetics 11, 283-290.
18. Karlin, S, Burge, C & Campbell, A M (1992) Statistical analyses of counts and distributions of restriction sites in DNA sequences. Nucleic Acids Research 20, 1363-1370.
19. Karlin, S, Mrazek, J & Campbell, A M (1996) Frequent oligonucleotides and peptides of the haemophilus influenzae genome. Nucleic Acids Research 24, 4263-4272.
20. Koonin, E V, Mushegian, A R & Rudd, K E (1996) Sequencing and analysis of bacterial genomes. Curr Biol 6, 404-416.
21. Brenner, S, Hubbard, T, Murzin, A & Chothia, C (1995) Gene Duplication in H. Influenzae. Nature 378, 140.
22. Riley, M (1997) Genes and proteins of Escherichia coli K-12 (GenProtEC). Nucleic Acids Res 25, 51-52.
23. Wolfe, K H & Shields, D C (1997) Molecular evidence for an ancient duplication of the entire yeast genome. Nature 387, 708-713.
24. Gerstein (1997) A Structural Census of Genomes: Comparing Eukaryotic, Bacterial and Archaeal Genomes in terms of Protein Structure. J. Mol. Biol. 274, 562-576.
25. Tamames, J, Casari, G, Ouzounis, C & Valencia, A (1997) Conserved clusters of functionally related genes in two bacterial genomes. J Mol Evol 44, 66-73.
26. Green, P, Lipman, D, Hillier, L, Waterston, R, States, D & Claverie, J M (1993) Ancient conserved regions in new gene sequences and the protein databases. Science 259, 1711-1716.
27. Koonin, E V, Tatusov, R L & Rudd, K E (1995) Sequence similarity analysis of Escherichia coli proteins: Functional and Evolutionary Implications. Proc. Natl. Acad. Sci. USA 92, 11921-11925.
28. Tatusov, R L, Koonin, E V & Lipman, D J (1997) A genomic perspective on protein families. Science 278, 631-637.
29. Ouzounis, C, Kyrpides, N & Sander, C (1995) Novel protein families in Archaean genomes. Nucl. Acids Res. 23, 565-570.
30. Clayton, R A, White, O, Ketchum, K A & Venter, J C (1997) The first genome from the third domain of life [news]. Nature 387, 459-462.
31. Bork, P, Ouzounis, C, Sander, C, Scharf, M, Schneider, R & Sonnhammer, E (1992) What's in a genome? Nature 358, 287.
32. Bork, P, Ouzounis, C, Sander, C, Scharf, M, Schneider, R & Sonnhammer, E (1992) Comprehensive sequence analysis of the 182 predicted open reading frames of yeast chromosome iii. Protein Science 1, 1677-1690.
33. Scharf, M, Schneider, R, Casari, G, Bork, P, Valencia, A, Ouzounis, C & Sander, C (1994). GeneQuiz: a workbench for sequence analysis, in Proceedings of the Second International Conference on Intelligent Systems for Molecular Biology. 348-353 (AAAI Press, Menlo Park, California).
34. Casari, G, et al. (1995) Challenging times for bioinformatics. Nature 376, 647-648.
35. Ouzounis, C, Bork, P, Casari, G & Sander, C (1995) New protein functions in yeast chromosome VIII. Protein Sci. 4, 2424-2428.
36. Gaasterland, T & Sensen, C W (1996) Fully automated genome analysis that reflects user needs and preferences. A detailed introduction to the MAGPIE system architecture. Biochimie 78, 302-310.
37. Huynen, M A, Diaz-Lazcoz, Y & Bork, P (1997) Differential genome display [letter]. Trends Genet 13, 389-390.
38. Tomb, J-F, et al. (1997) The complete genome sequence of the gastric pathogen Helicobacter pylori. Nature 388, 539-547.
39. Fraser, C M, et al. (1997) Genomic sequence of a Lyme disease spirochaete, Borrelia burgdorferi [see comments]. Nature 390, 580-586.
40. Karp, P, Riley, M, Paley, S & Pellegrini-Toole, A (1996) EcoCyc: Electronic Encyclopedia of E. coli Genes and Metabolism. Nucleic Acids Research 24, 32-40.
41. Mushegian, A R & Koonin, E V (1996) A minimal gene set for cellular life derived by comparison of complete bacterial genomes [see comments]. Proc Natl Acad Sci U S A 93, 10268-10273.
42. Koonin, E V, Tatusov, R L & Rudd, K E (1996) Protein Sequence Comparison at a Genome Scale. Meth. Enz. 266, 295-322.
43. Tang, C M, Hood, D W & Moxon, E R (1997) Haemophilus influence: the impact of whole genome sequencing on microbiology. Trends Genet 13, 399-404.
44. Tatusov, R L, et al. (1996) Metabolism and evolution of Haemophilus influenzae deduced from a whole- genome comparison with Escherichia coli. Curr Biol 6, 279-291.
45. Henikoff, S & Henikoff, J G (1993) Automated assembly of protein blocks for database searching. Proc. Natl. Acad. Sci. 19, 6565-6572.
46. Henikoff, S & Henikoff, J G (1994) Protein family classification based on searching a database of blocks. Genomics 19, 97-107.
47. Henikoff, S, Greene, E A, Pietrokovski, S, Bork, P, Attwood, T K & Hood, L (1997) Gene families: the taxonomy of protein paralogs and chimeras. Science 278, 609-614.
48. Henikoff, S, Pietrokovski, S & Henikoff, J G (1998) Superior performance in protein homology detection with the Blocks Database servers. Nucleic Acids Res 26, 309-312.
49. Sonnhammer, E L L & Kahn, D (1994) Modular arrangement of proteins as inferred from analysis of homology. Protein Science 3, 482-492.
50. Riley, M & Labedan, B (1997) Protein evolution viewed through Escherichia coli protein sequences: introducing the notion of a structural segment of homology, the module. J Mol Biol 268, 857-868.
51. Fabian, P, Murvai, J, Hatsagi, Z, Vlahovicek, K, Hegyi, H & Pongor, S (1997) The SBASE protein domain library, release 5.0: a collection of annotated protein sequence segments. Nucleic Acids Res 25, 240-243.
52. Corpet, F, Gouzy, J & Kahn, D (1998) The ProDom database of protein domain families. Nucleic Acids Res 26, 323-326.
53. Sonnhammer, E L, Eddy, S R, Birney, E, Bateman, A & Durbin, R (1998) Pfam: multiple sequence alignments and HMM-profiles of protein domains. Nucleic Acids Res 26, 320-322.
54. Sonnhammer, E L, Eddy, S R & Durbin, R (1997) Pfam: a comprehensive database of protein domain families based on seed alignments. Proteins 28, 405-420.
55. Tatusov, R L, Altschul, S F & Koonin, E V (1994) Detection of conserved segments in proteins: iterative scanning of sequence databases with alignment blocks. Proc Natl Acad Sci U S A 91, 12091-12095.
56. Bairoch, A, Bucher, P & Hofmann, K (1997) The PROSITE database, its status in 1997. Nucleic Acids Res 25, 217-221.
57. Attwood, T K, Beck, M E, Flower, D R, Scordis, P & Selley, J N (1998) The PRINTS protein fingerprint database in its fifth year. Nucleic Acids Res 26, 304-308.
58. Neuwald, A F, Liu, J S & Lawrence, C E (1995) Gibbs motif sampling: detection of bacterial outer membrane protein repeats. Protein Sci 4, 1618-1632.
59. Onuchic, J N, Luthey-Schulten, Z & Wolynes, P G (1997) Theory of protein folding: the energy landscape perspective. Annu Rev Phys Chem 48, 545-600.
60. Panchenko, A R, Luthey-Schulten, Z, Cole, R & Wolynes, P G (1997) The foldon universe: a survey of structural similarity and self- recognition of independently folding units. J Mol Biol 272, 95-105.
61. Panchenko, A R, Luthey-Schulten, Z & Wolynes, P G (1996) Foldons, protein structural modules, and exons. Proc Natl Acad Sci U S A 93, 2008-2013.
62. Gerstein, M & Altman, R (1995) Average core structures and variability measures for protein families: Application to the immunoglobulins. J. Mol. Biol. 251, 161-175.
63. Gerstein, M & Altman, R (1995) A Structurally Invariant Core for the Globins. CABIOS 11, 633-644.
64. Chothia, C & Lesk, A M (1986) The relation between the divergence of sequence and structure in proteins. EMBO J. 5, 823-826.
65. Chothia, C & Gerstein, M (1997) Protein evolution. How far can sequences diverge? Nature 385, 579-581.
66. Lesk, A M, Levitt, M & Chothia, C (1986) Alignment of amino acid sequences of distantly related proteins using variable gap penalties. Prot. Eng. 1, 77-78.
67. Brenner, S, Chothia, C & Hubbard, T (1998) Assessing sequence comparison methods with reliable structurally identified distant evolutionary relationships. Proc. Natl. Acad. Sci. USA 95, 6073-6078.
68. Dalal, S, Balasubramanian, S & Regan, L (1997) Protein alchemy: changing beta-sheet into alpha-helix [see comments]. Nat Struct Biol 4, 548-552.
69. Bork, P, Ouzounis, C & Sander, C (1994) From Genome Sequences to Protein Function. Curr. Opin. Struct. Biol. 4, 393-403.
70. Tomarev, S I, Zinovieva, R D & Piatigorsky, J (1992) Characterization of squid crystallin genes. Comparison with mammalian glutathione S-transferase genes. J Biol Chem 267, 8604-8612.
71. Wilks, H M, et al. (1988) A specific, highly active malate dehydrogenase by redesign of a lactate dehydrogenase framework. Science 242, 1541-1544.
72. Messerschmidt, A & Wever, R (1996) X-ray structure of a vanadium-containing enzyme: chloroperoxidase from the fungus Curvularia inaequalis. Proc Natl Acad Sci U S A 93, 392-396.
73. Simons, B H, Barnett, P, Vollenbroek, E G, Dekker, H L, Muijsers, A O, Messerschmidt, A & Wever, R (1995) Primary structure and characterization of the vanadium chloroperoxidase from the fungus Curvularia inaequalis. Eur J Biochem 229, 566-574.
74. Doolittle, R F (1994) Convergent evolution: the need to be explicit. Trends Biochem Sci 19, 15-18.
75. Lander, E S (1996) The Genomics: Global Views of Biology. Science 274, 536-539.
76. Remington, S J & Matthews, B W (1980) A systematic approach to the comparison of protein structures. J. Mol. Biol. 140, 77-99.
77. Satow, Y, Cohen, G H, Padlan, E A & Davies, D R (1986) Phosphocholine binding immunoglobulin Fab McPC603. An X-ray diffraction study at 2.7 A. J Mol Biol 190, 593-604.
78. Taylor, W R, Flores, T P & Orengo, C A (1994) Multiple Protein Structure Alignment. Prot. Sci. 3, 2358-2365.
79. Artymiuk, P J, Mitchell, E M, Rice, D W & Willett, P (1989) Searching Techniques for Databases of Protein Structures. J. Inform. Sci. 15, 287-298.
80. Sali, A & Blundell, T L (1990) The definition of general topological equivalence in protein structures: A procedure involving comparison of properties and relationships through simulated annealing and dynamic programming. J. Mol. Biol. 212, 403-428.
81. Vriend, G & Sander, C (1991) Detection of common three-dimensional substructures in proteins. Proteins 11, 52-58.
82. Russell, R B & Barton, G B (1992) Multiple Protein Sequence Alignment from Tertiary Structure Comparisons. Assignment of Global and Residue Level Confidences. Proteins 14, 309-323.
83. Holm, L & Sander, C (1993) Protein Structure Comparison by Alignment of Distance Matrices. J. Mol. Biol. 233, 123-128.
84. Grindley, H M, Artymiuk, P J, Rice, D W & Willett, P (1993) Identification of tertiary structure resemblance in proteins using a maximal common subgraph isomorphism algorithm. J Mol Biol 229, 707-721.
85. Godzik, A & Skolnick, J (1994) Flexible algorithm for direct multiple alignment of protein structures and sequences. CABIOS 10, 587-596.
86. Gibrat, J F, Madej, T & Bryant, S H (1996) Surprising similarities in structure comparison. Curr. Opin. Str. Biol. 6, 377-385.
87. Falicov, A & Cohen, F E (1996) A surface of minimum area metric for the structural comparison of proteins. Journal Of Molecular Biology 258, 871-892.
88. Feng, Z K & Sippl, M J (1996) Optimum superimposition of protein structures: ambiguities and implications. Fold Des 1, 123-132.
89. Cohen, G H (1997) ALIGN: A program to superimpose protein coordinates, accounting for insertions and deletions. J. Appl. Cryst. (in press).
90. Gerstein, M & Levitt, M (1998) Comprehensive Assessment of Automatic Structural Alignment against a Manual Standard, the Scop Classification of Proteins. Protein Science 7, 445-456.
91. Doolittle, R F (1987). Of Urfs and Orfs (University Science Books, Mill Valley, CA).
92. Gribskov, M & Devereux, J (1992). Sequence Analysis Primer (Oxford University Press, New York).
93. Taylor, W R & Orengo, C A (1989) Protein Structure Alignment. J. Mol. Biol. 208, 1-22.
94. Levitt, M & Gerstein, M (1998) A Unified Statistical Framework for Sequence Comparison and Structure Comparison. Proceedings of the National Academy of Sciences USA 95, 5913-5920.
95. Gerstein, M & Levitt, M (1996). Using Iterative Dynamic Programming to Obtain Accurate Pairwise and Multiple Alignments of Protein Structures, in Proc. Fourth Int. Conf. on Intell. Sys. Mol. Biol. 59-67 (AAAI Press, Menlo Park, CA).
96. Needleman, S B & Wunsch, C D (1971) A general method applicable to the search for similarities in the amino acid sequence of two proteins. J. Mol. Biol. 48, 443-453.
97. Johnson, M S, Sali, A & Blundell, T L (1990) Phylogenetic Relationships from Three-dimensional Protein Structures. Meth. Enz. 183, 670-691.
98. Orengo, C A, Flores, T P, Taylor, W R & Thornton, J M (1993) Identifying and Classifying Protein Fold Families. Prot. Eng. 6, 485-500.
99. Pascarella, S & Argos, P (1992) A Databank Merging Related Protein Structures and Sequences. Prot. Eng. 5, 121-137.
100. Orengo, C A (1994) Classification of protein folds. Curr. Opin. Struc. Biol. 4, 429-440.
101. Schmidt, R, Gerstein, M & Altman, R (1997) LPFC: An Internet Library of Protein Family Core Structures. Prot. Sci. 6, 246-248.
102. Altman, R, Hughes, C & Gerstein, M (1995) Methods for Displaying Macromolecular Structural Uncertainty: Application to the Globins. J. Mol. Graph. 13, 142-152.
103. Bryant, S H & Lawrence, C E (1993) An empirical energy function for threading protein sequence through the folding motif. Proteins Struct Funct Genet 16, 92-112.
104. Hobohm, U, Scharf, M, Schneider, R & Sander, C (1992) Selection of a representative set of structures from the Brookhaven Protein Data Bank. Protein Science 1, 409-417.
105. Hobohm, U & Sander, C (1994) Enlarged representative set of protein structures. Protein Science 3, 522.
106. Boberg, J, Salakoski, T & Vihinen, M (1992) Selection of a representative set of structures from Brookhaven Protein Data Bank. Proteins 14, 265-276.
107. Doolittle, R F (1995) The multiplicity of domains in proteins. [Review]. Annual Review of Biochemistry 64, 287-314.
108. Orengo, C A, Jones, D T & Thornton, J M (1994) Protein superfamilies and domain superfolds. Nature 372, 631-634.
109. Govindarajan, S & Goldstein, R A (1996) Why are some proteins structures so common? Proc Natl Acad Sci U S A 93, 3341-3345.
110. Li, H, Helling, R, Tang, C & Wingreen, N (1996) Emergence of preferred structures in a simple model of protein folding [see comments]. Science 273, 666-669.
111. Lipman, D J & Pearson, W R (1985) Rapid and sensitive protein similarity searches. Science 227, 1435-1441.
112. Altschul, S, Gish, W, Miller, W, Myers, E W & Lipman, D J (1990) Basic local alignment search tool. J. Mol. Biol. 215, 403-410.
113. Pearson, W R & Lipman, D J (1988) Improved Tools for Biological Sequence Analysis. Proc. Natl. Acad. Sci. USA 85, 2444-2448.
114. Bairoch, A & Apweiler, R (1998) The SWISS-PROT protein sequence data bank and its supplement TrEMBL in 1998. Nucleic Acids Res 26, 38-42.
115. Benson, D A, Boguski, M, Lipman, D J & Ostell, J (1996) Genbank. Nuc. Acid. Res. 24, 1-5.
116. Altschul, S F, Madden, T L, Schaffer, A A, Zhang, J, Zhang, Z, Miller, W & Lipman, D J (1997) Gapped BLAST and PSI-BLAST: a new generation of protein database search programs. Nucleic Acids Res 25, 3389-3402.
117. Abagyan, R A & Batalov, S (1997) Do aligned sequences share the same fold? J Mol Biol 273, 355-368.
118. Park, J, Teichmann, S A, Hubbard, T & Chothia, C (1997) Intermediate sequences increase the detection of homology between sequences. J Mol Biol 273, 349-354.
119. Gerstein, M (1998) Measurement of the Gain in Sensitivity in Transitive Sequence Comparison, through an Intermediate Sequence. Bioinformatics (in press).
120. Krogh, A, Brown, M, Mian, I S, Sjölander, K & Haussler, D (1994) Hidden Markov Models in Computational Biology: Applications to Protein Modelling. J. Mol. Biol. 235, 1501-1531.
121. Baldi, P, Chauvin, Y & Hunkapiller, T (1994) Hidden Markov Models of Biological Primary Sequence Information. Proc. Natl. Acad. Sci. 91,
122. Eddy, S R, Mitchison, G & Durbin, R (1994) Maximum Discrimination Hidden Markov Models of Sequence Consensus. J. Comp. Bio. 9, 9-23.
123. Taubes, G (1996) Software Matchmakers Help Make Sense of Sequences. Science 273, 588-590.
124. Bowie, J U, Lüthy, R & Eisenberg, D (1991) A Method to Identify Protein Sequences That Fold into a Known Three-Dimensional Structure. Science 253, 164-170.
125. Eddy, S R (1996) Hidden Markov models. Curr. Opin. Struc. Biol. 6, 361-365.
126. Gribskov, M, Lüthy, R & Eisenberg, D (1990) Profile Analysis. Meth. Enz. 183, 146-159.
127. Smith, T F & Waterman, M S (1981) Identification of common molecular subsequences. J. Mol. Biol. 147, 195-197.
128. Blattner, F R, et al. (1997) The Complete Genome Sequence of Escherichia coli K-12. Science 277, 1453-1462.
129. Goffeau, A, et al. (1996) Life with 6000 Genes. Science 274, 546-567.
130. Kim, J M, Vanguri, S, Boeke, J D, Gabriel, A & Voytas., D F (1998) Transposable elements and genome organization: a comprehensive survey of retrotransposons revealed by the complete Saccharomyces cerevisiae genome sequence. Genome Research In press.
131. Altschul, S F & Gish, W (1996) Local alignment statistics. Methods in Enzymology 266, 460-480.
132. Altschul, S F, Boguski, M S, Gish, W & Wootton, J C (1994) Issues in searching molecular sequence databases. [Review]. Nature Genetics 6, 119-129.
133. Karlin, S & Altschul, S F (1993) Applications and statistics for multiple high-scoring segments in molecular sequences. Proceedings of the National Academy of Sciences of the United States of America 90, 5873-5877.
134. Karlin, S, Bucher, P, Brendel, V & Altschul, S F (1991) Statistical methods and insights for protein and DNA sequences. Annu Rev Biophys Biophys Chem 20, 175-203.
135. Karlin, S & Altschul, S F (1990) Methods for assessing the statistical significance of molecular sequence features by using general scoring schemes. Proc Natl Acad Sci U S A 87, 2264-2268.
136. Pearson, W R (1998) Empirical statistical estimates for sequence similarity searches. J Mol Biol 276, 71-84.
137. Pearson, W R (1996) Effective Protein Sequence Comparison. Meth. Enz. 266, 227-259.
138. Pearson, W R (1997) Identifying distantly related protein sequences. Comput Appl Biosci 13, 325-332.
139. Brenner, S E & Hubbard, T J P (1995). A specification for defining and annotating regions of macromolecular structures., in Proc. 3rd Int. Conf. Intell. Sys. Mol. Biol. (eds. Rawlings, C, et al.) (AAAI Press, Menlo Park).
140. Brenner, S, Chothia, C, Hubbard, T J P & Murzin, A G (1996) Understanding Protein Structure: Using Scop for Fold Interpretation. Meth. Enz. 266, 635-642.
141. Frishman, D & Mewes, H-W (1997) PEDANTic genome analysis. Trends in Genetics 13, 415-416.
142. Bult, C J, et al. (1996) Complete Genome Sequence of the Methanogenic Archaeon, Methanococcus jannaschii. Science 273, 1058-1073.
143. Sonnhammer, E L & Durbin, R (1997) Analysis of protein domain families in Caenorhabditis elegans. Genomics 46, 200-216.
144. Ouzounis, C & Kyrpides, N (1996) The emergence of major cellular processes in evolution. FEBS Lett 390, 119-123.
145. Levitt, M & Chothia, C (1976) Structural patterns in globular proteins. Nature 261, 552-558.
146. Chothia, C, Hubbard, T, Brenner, S, Barns, H & Murzin, A (1997) Protein folds in the all-beta and all-alpha classes. Annu Rev Biophys Biomol Struct 26, 597-627.
147. Gerstein, M & Levitt, M (1997) A Structural Census of the Current Population of Protein Sequences. Proc. Natl. Acad. Sci. USA 94, 11911-11916.
148. Rost, B (1998) Marrying structure and genomics [In Process Citation]. Structure 6, 259-263.
149. Gerstein, M (1998) Comparing Genomes in terms of their Usage of Protein Folds. Proteins (submitted).
150. Velculescu, V E, et al. (1997) Characterization of the yeast transcriptome. Cell 88, 243-251.
151. Lashkari, D A, et al. (1997) Yeast microarrays for genome wide parallel genetic and gene expression analysis. Proc Natl Acad Sci U S A 94, 13057-13062.
152. DeRisi, J L, Iyer, V R & Brown, P O (1997) Exploring the metabolic and genetic control of gene expression on a genomic scale. Science 278, 680-686.
153. Bowie, J U & Eisenberg, D (1993) Inverted protein structure prediction. Curr Opin Struct Biol 3, 437-444.
154. Jones, D T & Thornton, J M (1996) Potential energy functions for threading. Curr. Opin. Struc. Biol. 6, 210-216.
155. Dubchak, I, Muchnik, I, Holbrook, S R & Kim, S H (1995) Prediction of protein folding class using global description of amino acid sequence. Proc Natl Acad Sci U S A 92, 8700-8704.
156. Gerstein, M, Sonnhammer, E & Chothia, C (1994) Volume Changes on Protein Evolution. J. Mol. Biol. 236, 1067-1078.
157. Altschul, S F, Carroll, R J & Lipman, D J (1989) Weights for Data Related by a Tree. J. Mol. Biol. 207, 647-653.
158. Sander, C & Schneider, R (1991) Database of Homology-Derived Protein Structures and the Structural Meaning of Sequence Alignment. Proteins: Struc. Func. Genet. 9, 56-68.
159. Vingron, M & Sibbald, P R (1993) Weighting in sequence space: A comparison of methods in terms of generalized sequences. Proc. Natl. Acad. Sci. USA 90, 8777-8781.
160. Miyazawa, S & Jernigan, R L (1996) Residue-residue potentials with a favorable contact pair term and an unfavorable high packing density term, for simulation and threading. J. Mol. Biol. 256, 623-644.
161. Wright, T Sampling and Census 2000: The Concepts. Am. Scientist 86, 245-253.
162. Thompson, S K (1992). Sampling (Wiley and Sons, New York).
163. Fischer, D & Eisenberg, D (1997) Assigning folds to the proteins encoded by the genome of mycoplasma genitalium [In Process Citation]. Proc Natl Acad Sci U S A 94, 11929-11934.
164. Rost, B (1996) PHD: Predicting One-dimensional Protein Secondary Structure by Profile-Based Neural Networks. Meth. Enz. 266, 525-539.
165. Defay, T & Cohen, F E (1995) Evaluation of current techniques for ab initio protein structure prediction. Proteins 23, 431-445.
166. Pedersen, J T & Moult, J (1997) Ab initio protein folding simulations with genetic algorithms: simulations on the complete sequence of small proteins. Proteins Suppl 1, 179-184.
167. Garnier, J, Gibrat, J F & Robson, B (1996) GOR method for predicting protein secondary structure from amino acid sequence. Meth. Enz. 266, 540-553.
168. Garnier, J, Osguthorpe, D & Robson, B (1978) Analysis of the accuracy and implications of simple methods for predicting the secondary structure of globular proteins. J. Mol. Biol. 120, 97-120.
169. Gibrat, J, Garnier, J & Robson, B (1987) Further developments of protein secondary structure prediction using information theory. J. Mol. Biol. 198, 425-443.
170. Rost, B & Sander, C (1993) Prediction of protein secondary structure at better than 70% accuracy. J. Mol. Biol. 232, 584-599.
171. Salamov, A & Solovyev, V (1995) Prediction of protein secondary structure by combining nearest-neighbor algorithms and multiple sequence alignments. J. Mol. Biol. 247, 11-15.
172. King, R D, Saqi, M, Sayle, R & Sternberg, M J (1997) DSC: public domain protein secondary structure predication. Comput Appl Biosci 13, 473-474.
173. Livingstone, C D & Barton, G J (1996) Identification of functional residues and secondary structure from protein multiple sequence alignment. Methods Enzymol 266, 497-512.
174. Russell, R B & Barton, G J (1993) The limits of protein secondary structure prediction accuracy from multiple sequence alignment. J Mol. Biol. 234, 951-957.
175. Engelman, D M, Steitz, T A & Goldman, A (1986) Identifying nonpolar transbilayer helices in amino acid sequences of membrane proteins. [Review]. Annual Review of Biophysics & Biophysical Chemistry 15, 321-353.
176. Kyte, J & Doolittle, R F (1982) A simple method for displaying the hydrophobic character of a protein. J. Mol. Biol. 157, 105-132.
177. Jähnig, F (1990) Structure predictions of membrane proteins are not that bad. TIBS 15, 93-95.
178. von Heijne, G (1994) Membrane proteins: from sequence to structure. Annu Rev Biophys Biomol Struct 23, 167-192.
179. von Heijne, G (1996) Principles of membrane protein assembly and structure. Prog Biophys Mol Biol 66, 113-139.
180. Persson, B & Argos, P (1994) Prediction of Transmembrane Segments in Proteins Utilising Multiple Sequence Alignments. J. Mol. Biol. 237, 182-192.
181. Jones, D T, Taylor, W R & Thornton, J M (1992) A new approach to protein fold recognition. Nature 358, 86-89.
182. Rost, B, Fariselli, P, Casadio, R & Sander, C (1995) Prediction of helical transmembrane segments at 95% accuracy. Prot. Sci. 4, 521-533.
183. Rost, B, Fariselli, P & Casadio, R (1996) Topology prediction for helical transmembrane segments at 95% accuracy. Prot. Sci. 7, 1704-1718.
184. Gerstein, M (1998) Structural Analysis of Genomes: How Representative are the Known Structures of the Proteins in a Complete Genome? Folding & Design (submitted).
185. Frishman, D & Mewes, H-W (1997) Protein structural classes in five complete genomes. Nature Struct. Biol. 4, 626-628.
186. Goffeau, A, Slonimski, P, Nakai, K & Risler, J L (1993) How Many Yeast Genes Code for Membrane-Spanning Proteins? Yeast 9, 691-702.
187. Arkin, I, Brunger, A & Engelman, D (1997) Are there dominant membrane protein families with a given number of helices? Proteins 28, 465-466.
188. Boyd, D, Schierle, C & Beckwith, J (1998) How many membrane proteins are there? Prot. Sci. 7, 201-205.
189. Jones, D T (1998) Do transmembrane protein superfolds exist? FEBS Lett 423, 281-285.
190. Tomb, J F, et al. (1997) The complete genome sequence of the gastric pathogen Helicobacter pylori [see comments] [published erratum appears in Nature 1997 Sep 25;389(6649):412]. Nature 388, 539-547.
191. Wallin, E & von Heijne, G (1998) Genome-wide analysis of integral membrane proteins from eubacterial, archaean, and eukaryotic organisms [In Process Citation]. Protein Sci 7, 1029-1038.
192. Knuth, D (1973). The Art of Computer Programming: vol 3, Sorting and Searching (Addison-Wesley, Reading, MA).
193. Konopka, A K & Martindale, C (1995) Noncoding DNA, Zipf's law, and language [letter]. Science 268, 789.
194. Flam, F (1994) Hints of a language in junk DNA [news] [see comments]. Science 266, 1320.
195. Bornberg-Bauer, E (1997) How are model protein structures distributed in sequence space? [In Process Citation]. Biophys J 73, 2393-2403.
196. Fleischmann, R D, et al. (1995) Whole-genome random sequencing and assembly of Haemophilus influenzae Rd [see comments]. Science 269, 496-512.
197. Fraser, C M, et al. (1995) The minimal gene complement of Mycoplasma genitalium [see comments]. Science 270, 397-403.
198. Bult, C J, et al. (1996) Complete genome sequence of the methanogenic archaeon, Methanococcus jannaschii [see comments]. Science 273, 1058-1073.
199. Kaneko, T, et al. (1996) Sequence analysis of the genome of the unicellular cyanobacterium Synechocystis sp. strain PCC6803. II. Sequence determination of the entire genome and assignment of potential protein-coding regions (supplement). DNA Res 3, 185-209.
200. Himmelreich, R, Hilbert, H, Plagens, H, Pirkl, E, Li, B C & Herrmann, R (1996) Complete sequence analysis of the genome of the bacterium Mycoplasma pneumoniae. Nucleic Acids Res 24, 4420-4449.
201. Blattner, F R, et al. (1997) The complete genome sequence of Escherichia coli K-12 [comment]. Science 277, 1453-1474.
202. Smith, D R, et al. (1997) Complete genome sequence of Methanobacterium thermoautotrophicum deltaH: functional analysis and comparative genomics. J Bacteriol 179, 7135-7155.
203. Kunst, F, et al. (1997) The complete genome sequence of the gram-positive bacterium Bacillus subtilis [see comments]. Nature 390, 249-256.
204. Klenk, H P, et al. (1997) The complete genome sequence of the hyperthermophilic, sulphate- reducing archaeon Archaeoglobus fulgidus. Nature 390, 364-370.
205. Deckert, G, et al. (1998) The complete genome of the hyperthermophilic bacterium Aquifex aeolicus. Nature 392, 353-358.
206. Kraulis, P J (1991) MOLSCRIPT - A program to produce both detailed and schematic plots of protein structures. J. Appl. Cryst. 24, 946-950.
207. Wootton, J C & Federhen, S (1996) Analysis of compositionally biased regions in sequence databases. Methods Enzymol 266, 554-571.
208. Wootton, J C (1994) Non-globular domains in protein sequences: automated segmentation using complexity measures. Comput Chem 18, 269-285.
Table 1, Current Microbial Genomes Available
|
Abbrev |
Genome |
Reference |
|
HI |
Haemophilus influenzae |
[196] |
|
MG |
Mycoplasma genitalium |
[197] |
|
MJ |
Methanococcus jannaschii |
[198] |
|
SS |
Synechocystis sp. |
[199] |
|
MP |
Mycoplasma pneumoniae |
[200] |
|
SC |
Saccharomyces cerevisiae |
[5] |
|
HP |
Helicobacter pylori |
[190] |
|
EC |
Escherichia coli |
[201] |
|
MT |
Methanobacterium thermoautotrophicum |
[202] |
|
BS |
Bacillus subtilis |
[203] |
|
AB |
Archaeoglobus fulgidus |
[204] |
|
BB |
Borrelia burgdorferi |
[39] |
|
AA |
Aquifex aeolicus |
[205] |
Table lists currently published microbial genomes, which are discussed in text. This table will rapidly be out of date, so it is probably best to consult a website, such as the TIGR microbial database (http://www.tigr.org/tdb/mdb/mdb.html) or our own genomes and structures site (http://bioinfo.mbb.yale.edu/genome).
Table 2, Common Folds Ranked by Duplication and Expression
|
Rep. Structure |
Genome Duplication |
Expression (aerobic) |
Expression (anaerobic) |
scop fold name |
|
1hcl |
1 |
3 |
4 |
Protein kinases (PK), cat. core |
|
1gky |
2 |
1 |
2 |
NTP Hydrolases with P-loop |
|
1ard |
3 |
9 |
5 |
Classic zinc finger |
|
2rn2 |
4 |
2 |
1 |
Ribonuclease H-like motif |
|
1xel |
5 |
4 |
3 |
Rossmann Fold |
|
125d |
6 |
6 |
7 |
Zn2/Cys6 DNA-binding dom. |
|
2bbk-H |
7 |
8 |
16 |
7-bladed beta-propeller |
|
1byb |
8 |
5 |
6 |
TIM-barrel |
|
1fxd |
9 |
7 |
10 |
like Ferrodoxin |
|
1enh |
10 |
30 |
36 |
DNA-binding 3-helical bundle |
|
… |
… |
|||
|
1lep-A |
17 |
10 |
9 |
GroES-like |
|
… |
… |
|||
|
1dkz-A |
22 |
11 |
8 |
like HSP70, Ct-dom. |
This table shows the most common folds in the yeast genome ranked according to a variety of criteria. Column 5 ("name") gives the scop name for the fold, as determined by scop [7] (In the table "dom" is used as an abbreviation for domain, "Nt-dom," for N-terminal domain, and "Ct-dom," for C-terminal domain.) Column 1 ("Rep. Struc.") gives a representative structure with this fold, including residue selection. Column 2 ("Duplication") gives an ordering of folds in terms of the number of times they are found in the yeast genome. For instance, the top fold (kinase) is found 110 times, while the second fold (NTP hydrolase) is found 69 times. Columns 3 and 4 ("expression") give an ordering of folds in terms of their degree of expression. Using the data from DeRisi et al. [152], the total expression E of a fold F is calculated as a sum of the expression levels of all the ORFs that contain this fold. The expression level of a given ORF (i.e. ORF i) is the degree of its "Red" color on a cDNA microarray R(i), less the background Rback(i), viz: ![]() . Column 3 gives the expression in aerobic conditions (high sugar, second time-series data point in DeRisi et al.), and Column 4, in anaerobic conditions (low sugar, high ethanol, last time-series data point in DeRisi et al.). Note how some folds that are in the top-10 in terms of duplication are not in this select list in terms of expression (e.g. "DNA-binding 3-helical bundle"). The table is adapted from [149]. It is available in its entirety (i.e. not just top-10) over the web at http://bioinfo.mbb.yale.edu/genome/browser/fold-report.
. Column 3 gives the expression in aerobic conditions (high sugar, second time-series data point in DeRisi et al.), and Column 4, in anaerobic conditions (low sugar, high ethanol, last time-series data point in DeRisi et al.). Note how some folds that are in the top-10 in terms of duplication are not in this select list in terms of expression (e.g. "DNA-binding 3-helical bundle"). The table is adapted from [149]. It is available in its entirety (i.e. not just top-10) over the web at http://bioinfo.mbb.yale.edu/genome/browser/fold-report.
Table 3, Overall Predicted Secondary Structure Composition
|
Total Number |
Frac. a.a. in... |
|||
|
ORFs |
a.a. |
strand |
helix |
|
|
Avg |
2206 |
775998 |
17% |
39% |
|
SD |
1731 |
1% |
2% |
|
|
EC |
4290 |
1358465 |
17% |
39% |
|
HI |
1680 |
505279 |
16% |
41% |
|
HP |
1577 |
500616 |
15% |
42% |
|
MG |
468 |
170400 |
17% |
39% |
|
MJ |
1735 |
497968 |
19% |
37% |
|
MP |
677 |
237905 |
17% |
39% |
|
SC |
6218 |
2900670 |
17% |
34% |
|
SS |
3168 |
1033450 |
16% |
38% |
Secondary structure composition of eight genomes, as predicted by the GOR program [167], applied to every amino acid (a.a.) in each genome. This gives a somewhat lower fraction of helix than in one just predicts the structure of the uncharacterized regions as defined in Figure 8. Genome names are defined in Table 1. Table is adapted from [184].
Figure 1, At What Structural Resolution do Organisms Differ?
Schematic illustrates a question involved in comparing genomes in terms of protein folds. Different organisms (e.g. a yeast and E. coli or a person and a plant) clearly appear morphologically distinct at macroscopic resolution (1 m to 10-6 m). However, they look the same at truly atomic resolution (~1 Å), where they are composed of similar proportions of the organic elements. At what resolution does one start to see differences?
Figure 2, Relationship between Sequence Similarity and Structural Similarity
This figure gives an updated version of Chothia & Lesk’s classic plot relating divergence in sequence to divergence in structure [64]. In the original plot Chothia & Lesk aligned 32 pairs of homologous structures (e.g. globins from two different species). For each pair they calculated a sequence similarity, in terms of a percentage of identical residues for aligned atoms ("PID"), and a structural similarity, expressed as the RMS deviation in alpha carbon positions of aligned atoms ("the RMS"). They found that the two quantities appeared to be highly related, following the relationship RMS = 0.4 exp (1.87 PID). To update this plot, we used a much larger data set, the scop classification of protein structure, version 1.35 [7]. This data set contains more than 14000 pairs of similar structure. (We used exactly 13967 pairs.) Instead of describing sequence similarity of each pair in terms of percentage identity, we used the more modern statistical language, the P-value [94, 136]. Then depending on whether or not a given pair had any appreciable sequence similarity, we aligned it, either using standard Needleman-Wunsch sequence comparison or a structural alignment program [90, 96], and did a least-squares fit based on the aligned atoms. This allowed us to characterize the structural similarity of the pair with two numbers, an RMS and the number of aligned atoms (N). For all the pairs within a range of sequence alignment scores (i.e. a bin), we calculated various RMS statistics, mean, median, and top and bottom quartile. Finally, we graphed these quantities versus sequence similarity (P-value). This plot shows a similar relationship between sequence and structure as in the original work of Chothia & Lesk.
Figure 3, A Fold Template
TOP-LEFT shows a structural alignment of two similar protein structures (globins). TOP-RIGHT shows how a number of aligned structures can be fused into a "fold template," where the variability at each aligned position is represented with an "uncertainty ellipsoid." A large number of these fold templates could constitute a fold library. BOTTOM shows the fold template in terms of sequence. Note how the conserved, "core" regions are disjoint in terms of sequence.
Figure 4, The Range of Structural Similarities
LEFT, An easy to align pair, two globins. The aligned positions are indicated by small, gray CPK spheres. Most of the residues are aligned correctly. CENTER, A harder to align pair, an immunoglobulin light-chain variable domain (d7fabl2) and an immunoglobulin constant domain (d1reia1). RIGHT, A very hard to align pair, the C-terminal domain of C-terminal domain glyceraldehyde-3-phosphate dehydrogenase. The left half of the subfigure shows wire frames, which illustrate how hard the relationship is to see. These structures (d1gd1o2 in the TOP-HALF and d1dpga2 at BOTTOM-HALF) are considered to share the fold. This is highlighted in the ribbon diagram (RIGHT-RIGHT) and indicated in the topology diagram. This figure is adapted from [90].
Figure 5, Distribution of Known Folds amongst the Genomes
This figure is adapted from [24, 147]. At the time this analysis was done there were 300 known folds, somewhat less than at present (~350). TOP, of the total 300 folds, 148 appear in the 3 genomes, with 45 shared between all three. The abbreviations for the three genomes are shown in Table 1. Most of the folds are either in the HI or SC genomes, even though the HI genome is smaller the MJ one. This reflects the bias in the structure databank. BOTTOM shows how the 300 folds are distributed amongst ALL bacterial and eukaryotic sequences, showing how representative a genome is for a whole kingdom.
Figure 6, Five Folds common in All Three Kingdoms
The figure shows five basic molecular parts, five folds that are shared by SC, HI, and MJ and are common in each of the three genomes. Here "commonness" is determined by the average frequency rank of the fold over each of the three genomes. All folds are drawn with molscript [206]. Also shown are highly schematic views of the sheet topology. Boxes indicate parallel strands in a beta-sheet with their order noted. (Strands are coming out of the page.) Solid arcs joining the boxes indicate right-handed connections between the parallel strands. All of these involve skipping no more than 2 strands and are through a parallel helix packed onto the sheet, from above or below. Half of an arc indicates that there is a parallel helix connected to either the first or last strand of the sheet. There is one exceptional connection, indicated with a dotted line: In the Rossmann fold there is a connection across 3 strands through a parallel helix. This figure is adapted from [24].
Figure 7, Issues Associated with the Multi-domain Nature of Proteins
This schematic highlights that fact that a given ORF can contain many structural features. TOP, Various regions of a representative ORF are annotated with different structural features, such as transmembrane helices or homology to known structure. Sometimes these features overlap, as is often the case for TM-helices and low-complexity regions. After "masking" the first four structural features (PDB matches, low-complexity regions, TM-helices, and linkers), one is left with uncharacterized regions, which can be characterized by a limited amount of structure prediction. BOTTOM shows that having multiple domains introduces complexity in clustering sequences. Naively applied single-linkage clustering will group together two sequences (i.e. 2 and 4) that have similarity to different domains (B and C) in a third, intermediate sequence (3). TOP is adapted from [24].
Figure 8, When will all Structures in Genome be Known?
This figure attempts to determine when all the structures will be known for the proteins in a complete genome. The TOP panel shows how the fraction of amino acids characterized in eight genomes increases each year with the addition of new structures to the PDB -- imagining that the complete sequences of the eight genomes were known a quarter century ago. A loose "back-of-the-envelope" trendline is fit to the increase in the last decade. In the BOTTOM panel, this trendline is extrapolated to the point when all structures in the genomes are known, which is rather pessimistically estimated to be around 2050. Characterized regions are structural features, as shown Figure 7. They are either PDB matches (as determined by the FASTA program), TM-helices (identified as described in figure 9), low-complexity regions (identified using the SEG program [207, 208]), or linkers (short stretches of less than 50 residues linking two the previous elements). Abbreviations for the genomes are in Table 1.
Figure 9, Transmembrane Folds in Microbial Genomes
This log-log graph shows the occurrence of membrane proteins with a given number of transmembrane (TM) helices in each of the eight genomes. Abbreviations are defined in Table 1. The occurrence drops off in a similar fashion in all eight genomes, according to a Zipf-like law, and a fit to all eight is shown in the graph. The transmembrane segments were identified using the GES hydrophobicity scale [175]. Figure is adapted from [149].
Figure 10, Scale of the Data: Molecular Biology vs. Other Disciplines
Schematic illustrates the scale of the fundamental data set in molecular biology, the table of folds, in comparison to data sets in other disciplines. The table of folds is expected to contain between 1000 and 10000 objects. This is larger in scale than the fundamental data in physics and chemistry (~10 fundamental constants in physics and ~100 elements in chemistry), about the same size as a fundamental data set in finance (the ~1000-10000 companies traded on the stock market), and smaller than data sets commonly used in politics and demographics (>1,000,000 individuals in a state).
Fig. 1
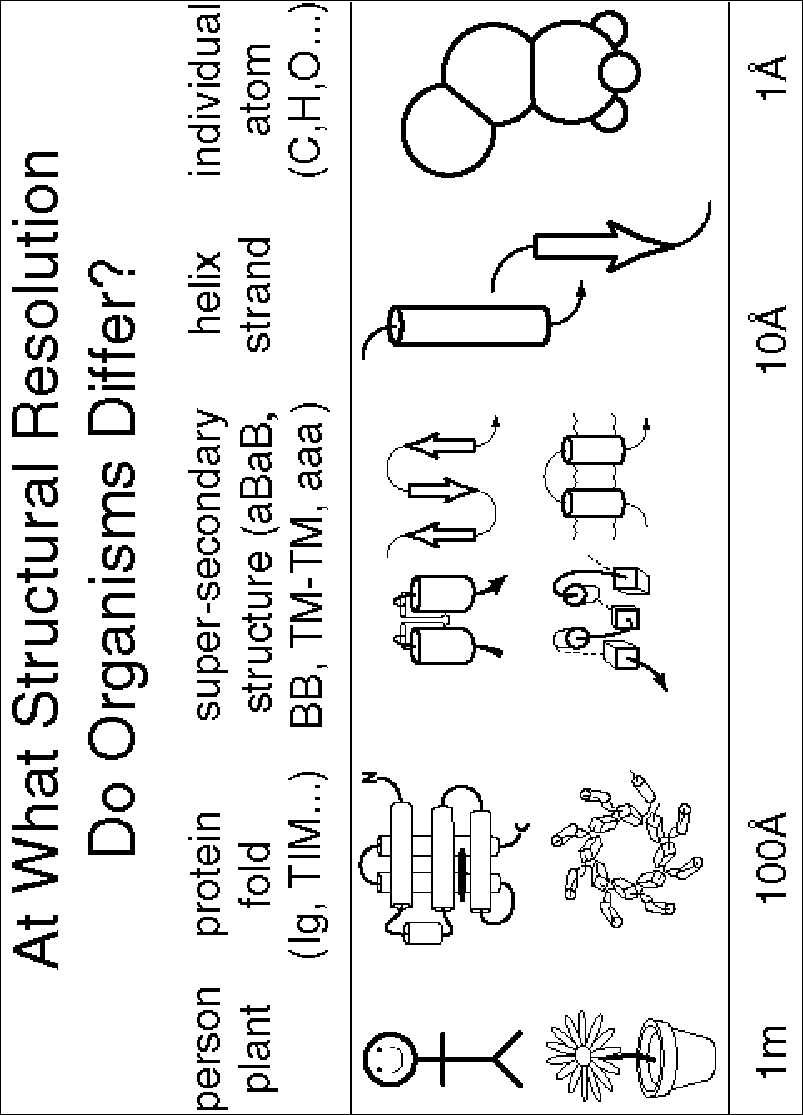
Fig. 2
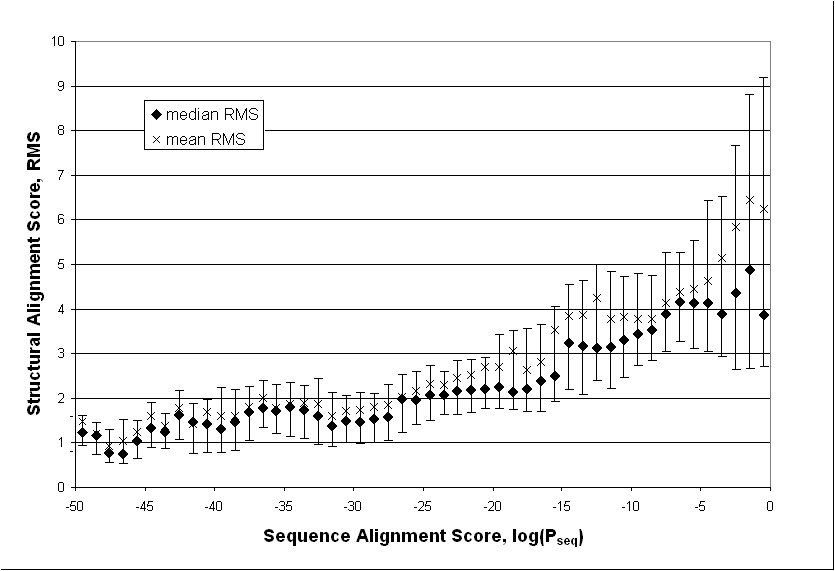
Fig. 3

Fig. 4
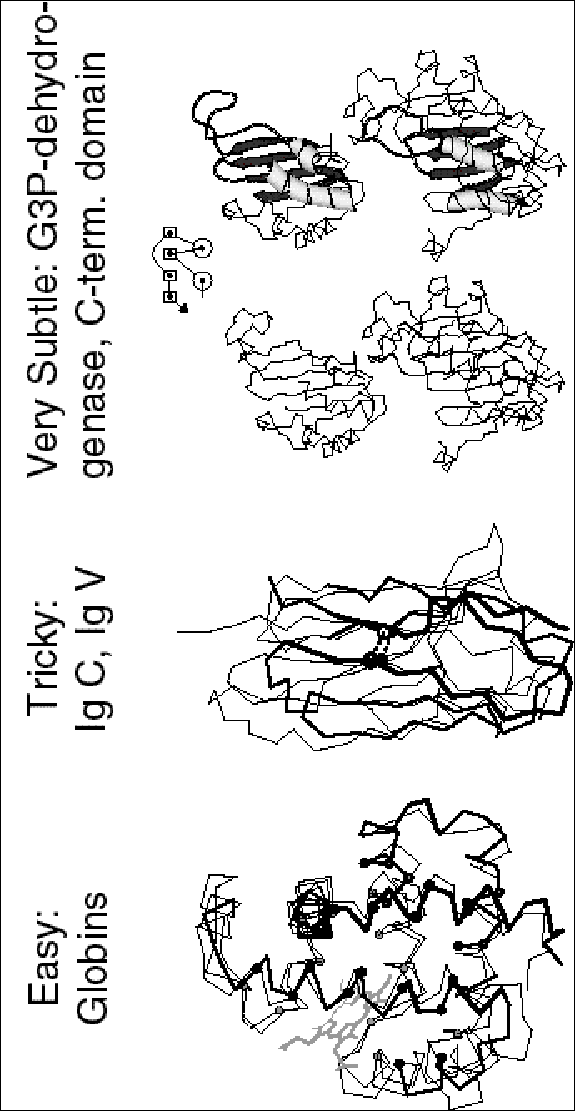
Fig. 5
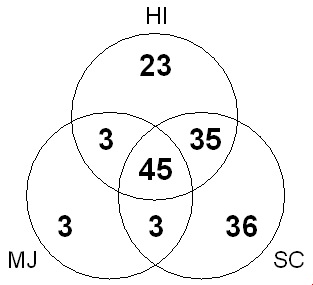
Fig. 6
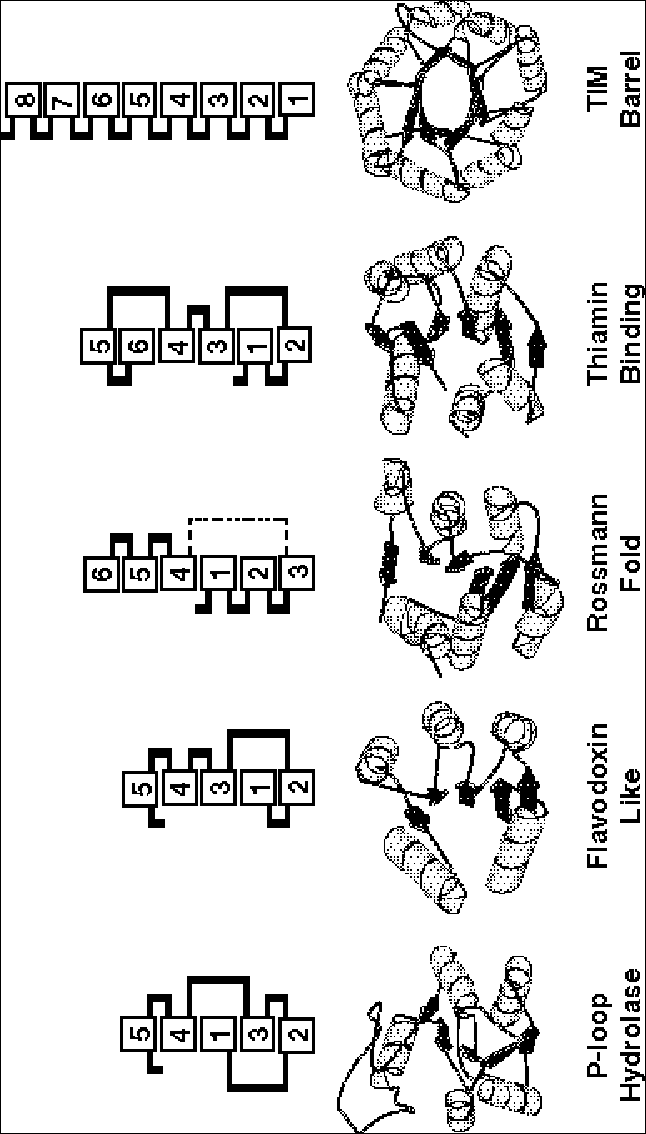
Fig. 7
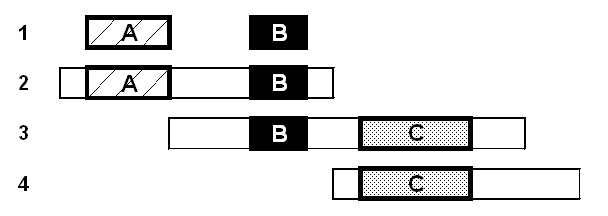
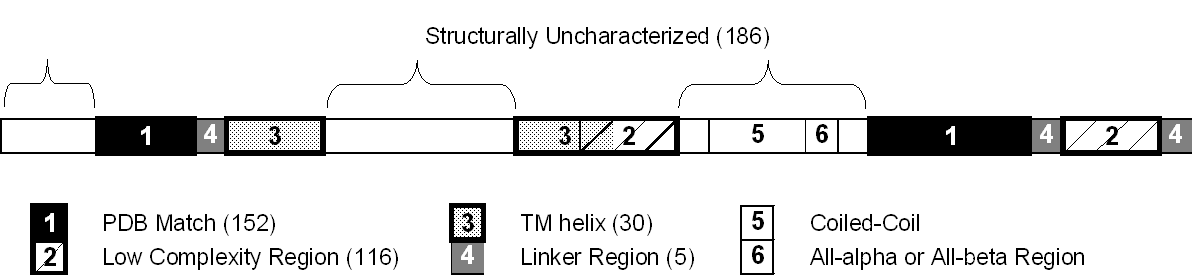
Fig. 8
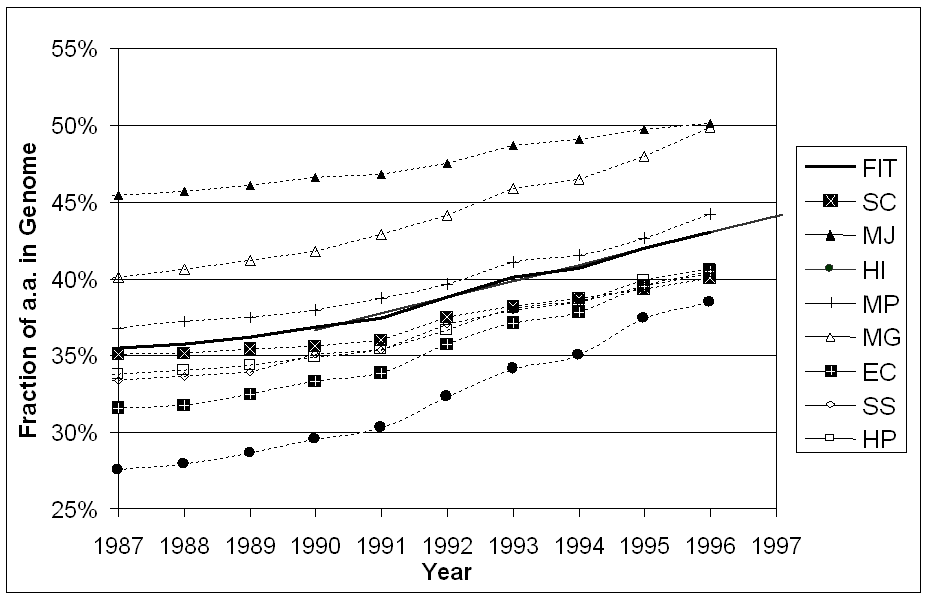
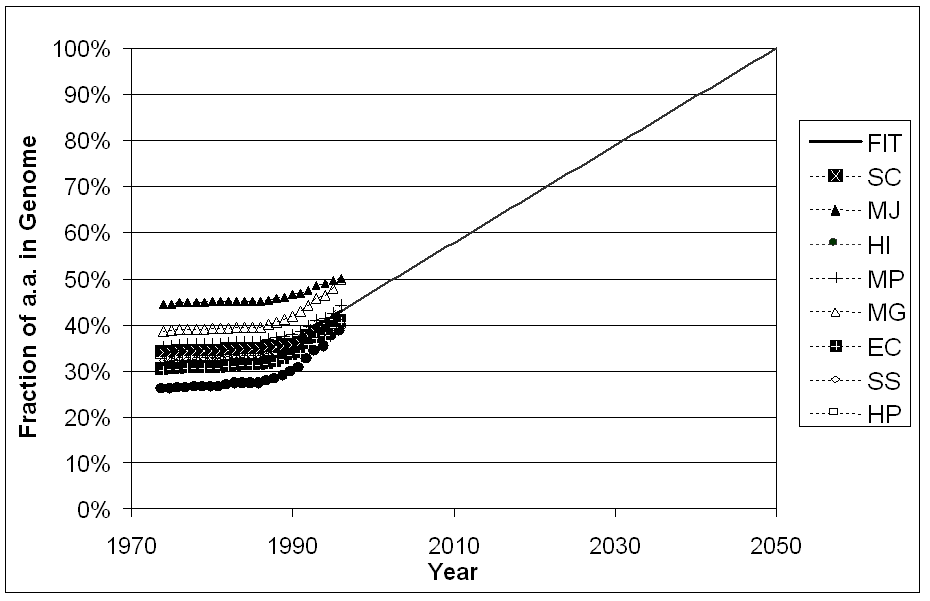
Fig. 9
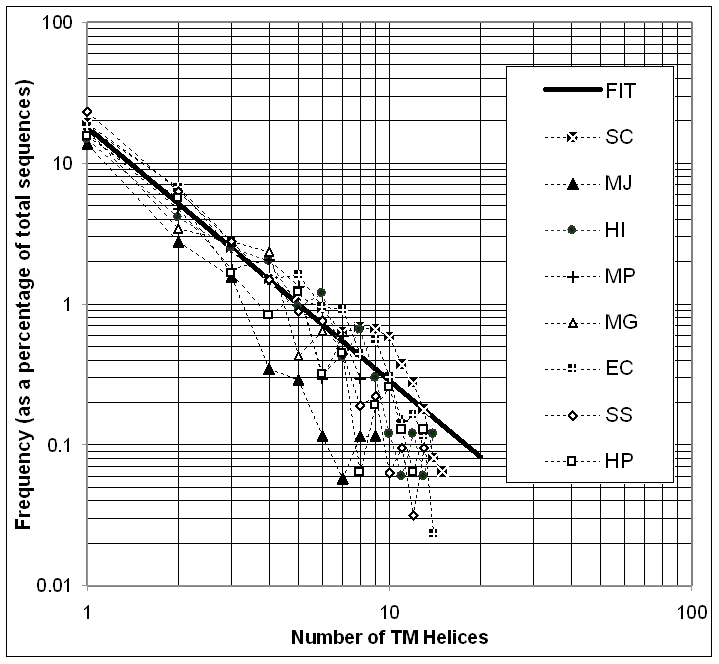
Fig. 10