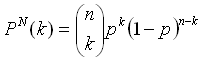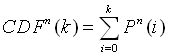STUDYING MACROMOLECULAR MOTIONS IN A DATABASE FRAMEWORK: FROM STRUCTURE TO SEQUENCE
Mark Gerstein,1 Ronald Jansen,1
Ted Johnson,1 Jerry Tsai,2 and Werner Krebs1
1
Department of Molecular Biophysics and Biochemistry
Yale University, 266 Whitney Avenue
New Haven, CT 06511
2
Department of Structural Biology, Stanford University
Stanford, CA 94305
ABSTRACT
We describe database approaches taken in our lab to the study of protein and nucleic acid motions. We have developed a database of macromolecular motions, which is accessible on the World Wide Web with an entry point at http://bioinfo.mbb.yale.edu/MolMovDB. This attempts to systematize all instances of macromolecular movement for which there is at least some structural information. At present it contains detailed descriptions of more than 100 motions, most of which are of proteins. Protein motions are further classified hierarchically into a limited number of categories, first on the basis of size (distinguishing between fragment, domain, and subunit motions) and then on the basis of packing. Our packing classification divides motions into various categories (shear, hinge, other) depending on whether or not they involve sliding over a continuously maintained and tightly packed interface. We quantitatively systematize the description of packing through the use of Voronoi polyhedra and Delaunay triangulation. In addition to the packing classification, the database provides some indication about the evidence behind each motion (i.e. the type of experimental information or whether the motion is inferred based on structural similarity) and attempts to describe many aspects of a motion in terms of a standardized nomenclature (e.g. the maximum rotation, the residue selection of a fixed core, etc). Currently, we use a standard relational design to implement the database. However, the complexity and heterogeneity of the information kept in the database makes it an ideal application for an object-relational approach, and we are moving it in this direction. The database, moreover, incorporates innovative Internet cooperatively features that allow authorized remote experts to serve as database editors. The database also contains plausible representations for motion pathways, derived from restrained 3D interpolation between known endpoint conformations. These pathways can be viewed in a variety of movie formats, and the database is associated with a server that can automatically generate these movies from submitted coordinates. Based on the structures in the database we have developed sequence patterns for linkers and flexible hinges and are currently using these for the annotation of genome sequence data.
INTRODUCTION
Motion is frequently the way macromolecules (proteins and nucleic acid) carry out particular functions; thus motion often serves as an essential link between structure and function. In particular, protein motions are involved in numerous basic functions such as catalysis, regulation of activity, transport of metabolites, formation of large assemblies and cellular locomotion. In fact, highly mobile proteins have been implicated in a number of diseases—e.g., the motion of gp41 in AIDS and that of the prion protein in scrapie. Another reason for the study of macromolecular motions results from their fundamental relationship to the principles of protein and nucleic acid structure and stability.
Macromolecular motions are amongst the most complicated biological phenomena that can be studied in great quantitative detail, involving concerted changes in thousands of precisely specified atomic coordinates. Fortunately, it is now possible to study these motions in a database framework, by analyzing and systematizing many of the instances of protein structures solved in multiple conformations. We summarize here some recent work in our laboratory relating to the construction of a database of protein motions) and the use of Voronoi polyhedra to study packing. We also present some preliminary results relating to creating sequence patterns for hinges and flexible linkers.
|
|


|
|
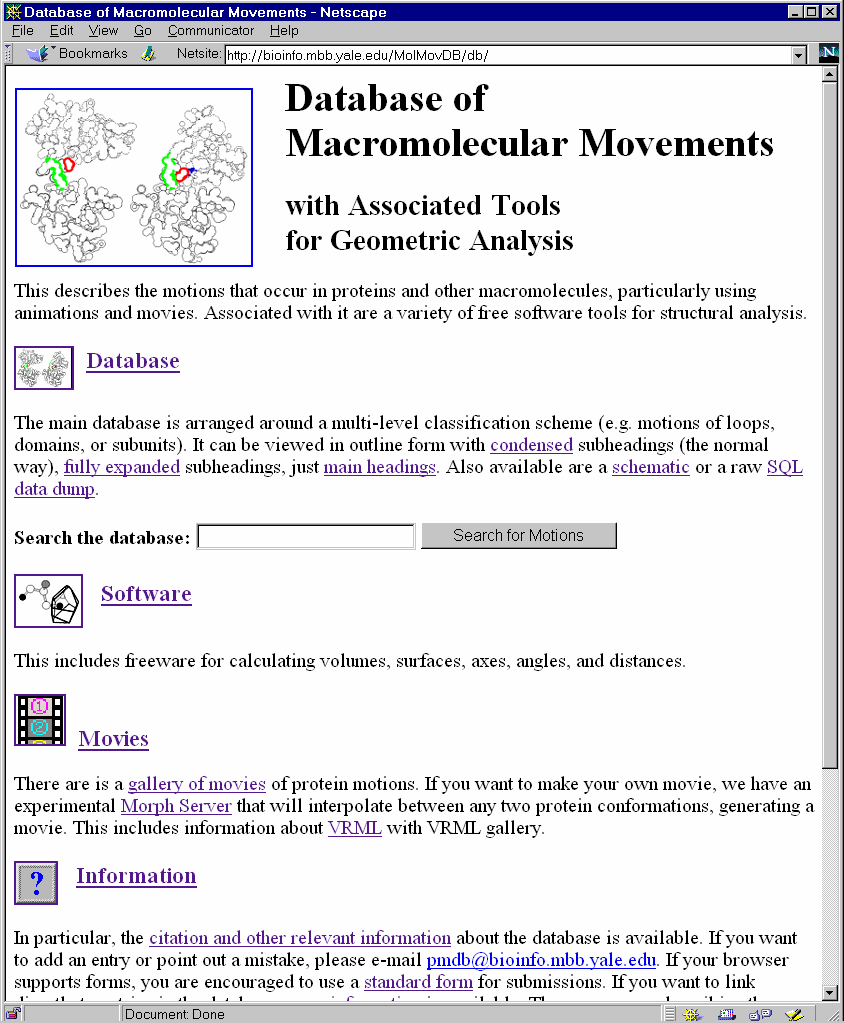
Figure 1 . The Motions Database on the Web. LEFT shows the World Wide Web "home page" of the database. One can type keywords in the small box at the top to retrieve entries. RIGHT shows an entry retrieved by such a keyword search (the entry for calmodulin). Graphics and movies are accessed by clicking on an entry page. (These have been deliberately segregated from the textual parts of the database since the interface was designed to make it easy to use on a low-bandwidth, text-only browser, e.g. lynx or the original www_3.0.) The main URL for the database is http://bioinfo.mbb.yale.edu/MolMovDB. Beneath this are pages listing all the current movies, graphics illustrating the use of VRML to represent endpoints, and an automated submission form to add entries to the database. The database has direct links to the PDB for current entries (http://www.pdb.bnl.gov); the obsolete database (http://pdbobs.sdsc.gov) for obsolete entries; scop (http://scop.mrc-lmb.cam.ac.uk); Entrez/PubMed (http://www.ncbi.nlm.nih.gov/PubMed/medline.html); and LPFC (http://smi-web.stanford.edu/projects/helix/LPFC). Through these links one can easily connect to other common protein databases such Swiss-Prot, Pro-Site, CATH, RiboWeb, and FSSP . |
The Database
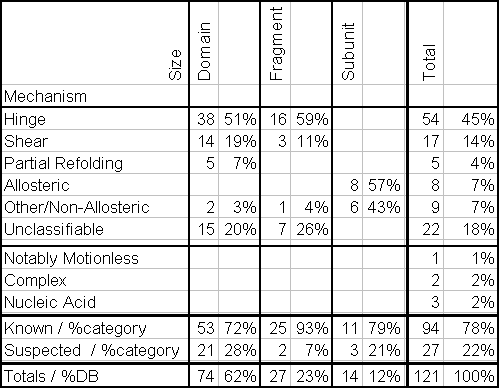
The primary public interface to the database consists of coupled hypertext documents available over the World Wide Web at http://bioinfo.mbb.yale.edu/MolMovDB. As shown in Figure 1, use of the web interface is straightforward and simple. The database may be browsed either by typing various search keywords into the main page or by navigating through an outline. Either way brings one to the entries. Thus far, the database has ~120 entries, which reference over 240 structures in the Protein Databank (PDB) (Table 1).
Unique Motion Identifier
Each entry is indexed by a unique motion identifier, rather than around individual proteins and nucleic acids. This is necessary because a single macromolecule can not only have a number of motions, but the essential motion can be shared amongst a number of different macromolecules.
Attributes of a Motion
In addition to the motion identifier, each entry has the following information:
Structures. Brookhaven Protein DataBank (PDB) identifiers are given for the various conformations of the macromolecule (e.g. open and closed). The identifiers have been made into hypertext links directly to the structure entries in the main protein and nucleic acid databases (PDB and NDB) and to sequence and journal cross-references via the Entrez and MMDB databases. Links are also made to related structures via the Structural Classification of Proteins (SCOP).
Literature. Literature references are given. Where possible these are via Medline unique identifiers, allowing a link to be made into the PubMed database.
Documentation. Each entry has a paragraph or so of plain text documentation. While this is, in a sense, the least precisely defined field, it is the heart of each entry, describing the motion in intelligible prose and referring to figures, where appropriate.
Standardized Nomenclature. For many entries we describe the overall motion using standardized numeric terminology, such as the maximum displacement (overall and of just backbone atoms) and the degree of rotation around the hinge. These statistics are summarized in Table 2. We also attempt to give the transformations (from ii) needed to optimally superimpose and orient each coordinate set to best see the motion (i.e. down screw-axis) and the selections of residues with large changes in torsion angles, packing efficiency, or neighbor contacts.
Graphics. Many entries have links to graphics and movies describing the motion, often depicting a plausible interpolated pathway (see below).
HIERARCHICAL CLASSIFICATION SCHEME BASED ON SIZE THEN PACKING
Size Classification: Fragment, Domain, Subunit
The most basic division in the current classification scheme is between proteins and nucleic acids. There are currently far fewer nucleic-acid motion entries than those of proteins, reflecting the much larger number of known protein structures. At present, the database includes the nucleic-acid motions evident from comparing various conformations of the known structures of catalytic RNAs and tRNAs (specifically, the Hammerhead ribozyme, the P4-P6 domain of the Group II intron, and Asp-tRNA).
The classification scheme for proteins has the hierarchical layout shown in Figure 2. The basic division is based on the size of the motion. Ranked in order of their size, protein movements fall into three categories: the motions of fragments smaller than domains, domains, and subunits.
Nearly all large proteins are built from domains, and domain motions, such as those observed in hexokinase or citrate synthase, provide the most common examples of protein flexibility. The motion of fragments smaller than domains usually refers to the motion of surface loops, such as the ones in triose phosphate isomerase or lactate dehydrogenase, but it can also refer to the motion of secondary structures, such as of the helices in insulin. Often domain and fragment motions involve portions of the protein closing around a binding site, with a bound substrate stabilizing a closed conformation. They, consequently, provide a specific mechanism for induced-fit in protein recognition. In enzymes this closure around a binding site has been analyzed in particular detail. It serves to position important chemical groups around the substrate, shielding it from water and preventing the escape of reaction intermediates.
Subunit motion is distinctly different from fragment or domain motion. It affects two large sections of polypeptide that are not covalently connected. It is frequently part of an allosteric transition and tied to regulation. The relative motions of the subunits in the transport protein hemoglobin and the enzyme glycogen phosphorylase change the affinity with which these proteins bind to their primary substrates and are good examples.
Packing Classification: Hinge and Shear
For protein motions of domains and smaller units, we have systematized the motions on the basis of packing, using a scheme developed previously. This is because the tight packing of atoms inside of proteins provides a most fundamental constraint on protein structure. Unless there is a cavity or packing defect, it is usually impossible for an atom inside a protein to move much without colliding with a neighboring atom.
Internal interfaces between different parts of a protein are packed very tightly. Furthermore, they are not smooth, but are formed from interdigitating sidechains. Common sense consideration of these aspects of interfaces places strong constraints on how a protein can move and still maintain its close packing. Specifically, maintaining packing throughout a motion implies that the sidechains at the interface must maintain their same relative orientation and pattern of inter-sidechain contacts in both conformations (e.g. open and closed).
These straightforward constraints on the types of motions that are possible at interfaces allow an individual movement within a protein to be described in terms of two basic mechanisms, shear and hinge, depending on whether or not it involves sliding over a continuously maintained interface (Figure 2). A complete protein motion (which can contain many of these smaller "movements") can be built up from these basic mechanisms. For the database, a motion is classified as shear if it predominately contains shear movements and as hinge if it is predominately composed of hinge movements. More detail on the characteristics of the two types of motion follows.
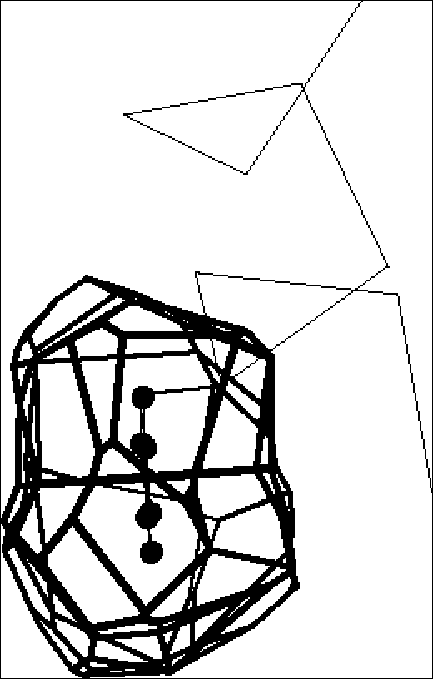
Shear. As shown in Figure 3, the shear mechanism basically describes the special kind of sliding motion a protein must undergo if it wants to maintain a well-packed interface. Because of the constraints on interface structure described above, individual shear motions have to be very small. Sidechain torsion angles maintain the same rotamer configuration (with <15° rotation of sidechain torsions); there is no appreciable mainchain deformation; and the whole motion is parallel to the plane of the interface, limited to total translations of ~2 Å and rotations of 15°. Since an individual shear motion is so small, a single one is not sufficient to produce a large overall motion, and a number of shear motions have to be concatenated to give a large effect — in a similar fashion to each plate in a stack of plates sliding slightly to make the whole stack lean considerably. Examples include the Trp repressor and aspartate amino transferase.
Hinge. As shown in Figure 4, hinge motions occur when there is no continuously maintained interface constraining the motion. These motions usually occur in proteins that have two domains (or fragments) connected by linkers (i.e. hinges) that are relatively unconstrained by packing. A few large torsion angle changes in the hinges are sufficient to produce almost the whole motion. The rest of the protein rotates essentially as a rigid body, with the axis of the overall rotation passing through the hinges. The overall motion is always perpendicular to the plane of the interface (so the interface exists in one conformation but not in the other, as in the closing and opening of a book) and is identical to the local motion at the hinge. Examples include lactoferrin and tomato bushy stunt virus (TBSV).
Gerstein et al. analyzed the hinged domain and loop motion in specific proteins (lactate dehydrogenase, adenylate kinase, lactoferrin). These studies emphasized how critical the packing at the base of a protein hinge is (in the same sense that the "packing" at the base of an everyday door hinge determines whether or not the door can close). Protein hinges are special regions of the mainchain in the sense that they are exposed and have few packing constraints on them and are thus free to sharply kink (Figure 4). Most mainchain atoms, in contrast, are usually buried beneath layers of other atoms (usually sidechain atoms), precluding large torsion angle changes and hinge motions.
It is important to note that because most shear motions do, in fact, contain hinges, (joining the various sliding parts) the existence of a hinge is not the salient difference between the two basic mechanisms. Instead, it is the existence of a continuously maintained interface.
Other Classification
Most of the fragment and domain motions in the database fall within the hinge-shear classification. However, we have created additional categories to deal with the small number of exceptions.
Data Entry
One innovative feature of the database is that it allows authorized remote researchers to enter motions in their area of expertise directly into the database via a Web form. Authorization to edit a given motion entry, if necessary, works in conjunction with the standard password feature built into modern Web browser systems. The layout of the Web form is analogous to that of a normal HTML page describing a motion in the database, except that the various fields have been replaced by textboxes and pull-down selectors to make the Web page editable. The user retrieves either a blank form or a form corresponding to a pre-existing motion entry, makes appropriate changes remotely over the Internet via his or her Web browser, and then simply clicks the ‘Submit’ button to save changes into the database. Depending on whether or not the user has editing privileges over a particular motion entry, the changes may be published immediately or upon further approval by the database maintainers. The remote user may immediately preview the edited motion entry to see what it will look like once it becomes public.
The Web form system (Figure 5) takes advantage of advanced features of the Informix Dynamic Server with Universal Option to enable user previews. The Web Datablade module allows database content to be dynamically and rapidly translated into Web content with little additional overhead compared to static pages. Because updates to the database can be translated instantaneously into updated Web content, remote editors are able to preview their changes as it will appear to the end database user instantaneously before submitting or publishing them. Previously, we stored the database using the MSQL database software package, which is freely available to academic users. Unlike the commercial Informix system, the MSQL package does not support Application Program Interfaces (APIs) that allow for an efficient, rapid translation of database content into Web content. Consequently, it was necessary to store the Web interfaces as static HTML files on the server. For Web content to remain current, these pages would need to be rebuilt each time the database changed, a time-consuming process that would have prevented accurate previews. In addition, the Informix database system also features state-of-the-art transaction concurrency and logging, important features when multiple users are simultaneously updating the database.
In this way, the database takes full advantage of the cooperatively features of the Internet and modern database software, allowing experts in distant parts of the world to collaborate simultaneously on macromolecular motions. In addition to accelerating the rate at which the database may be populated, this feature improves the accuracy and timeliness of existing database entries by allowing them to be edited, revised, and updated, if necessary, by experts in the field.
Internet Hits
The database is currently receiving over 65,000 hits from over 45,000 sites each month. Internet traffic on the database’s main web server grew approximately exponentially between November, 1997, and February 1998, with database usage doubling approximately every other month during this period. In recent months, database usage has continued to grow, albeit at a somewhat reduced rate. We expect this trend to continue as the database becomes established in the structural biology community.
Standardized Tools For Protein Motions
Quantification of packing using Voronoi polyhedra
Packing clearly is an essential component of the motions classification. Often this concept is discussed loosely and vaguely by crystallographers analyzing a particular protein structure—for instance, "Asp23 is packed against Gly38" or "the interface between domains appears to be tightly packed." We have attempted to systematize and quantify the discussion of packing in the context of the motions database through the use of particular geometric constructions called Voronoi polyhedra and Delaunay triangulation.
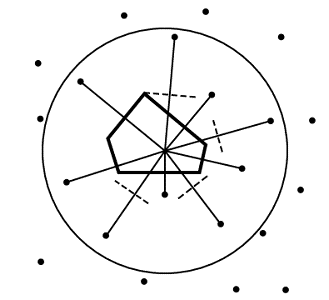
Voronoi polyhedra are a useful way of partitioning space amongst a collection of atoms. Each atom is surrounded by a single convex polyhedron and allocated the space within it (Figure 6). The faces of Voronoi polyhedra are formed by constructing dividing planes perpendicular to vectors connecting atoms, and the edges of the polyhedra result from the intersection of these planes.
Voronoi polyhedra were originally developed (obviously enough) by Voronoi nearly a century ago. Bernal and Finney used them to study the structure of liquids in the 1960s. However, despite the general utility of these polyhedra, their application to proteins was limited by a serious methodological difficulty: while the Voronoi construction is based around partitioning space amongst a collection of "equal" points, all protein atoms are not equal: some are clearly larger than others (e.g. sulfur versus oxygen). Richards found a solution to this problem and first applied Voronoi polyhedra to proteins in 1974. He has, subsequently, reviewed their use in this application.
Voronoi polyhedra are particularly useful in studying the packing of the protein interior. This is because the construction of Voronoi polyhedra allocates all space amongst a collection of atoms; there are no gaps as there would be if one, say, simply drew spheres around the atoms. Thus, the volume of cavities or defects between atoms are included in their Voronoi volume, and one finds that the packing efficiency is inversely proportional to the size of the polyhedra. This indirect measurement of cavities contrasts with other types of calculations that measure the volume of cavities explicitly. Moreover, since protein interiors are tightly packed, fitting together like a jig-saw puzzle, the various types of protein atoms occupy well-defined amounts of space. This fact has made the calculation of standard volumes for residues in proteins a worthwhile proposition.
Voronoi polyhedra calculations have been applied to other aspects of packing in protein structure. In particular, they have been used to study protein-protein recognition, protein motions, and the protein surface. As the Voronoi volume of an atom is a weighted average of the distances to all its neighbors (where the contact area with a neighbor is the weight), Voronoi polyhedra are very useful in assessing interatomic contacts. Furthermore, the faces of Voronoi polyhedra have been used to characterize protein accessibility and to assess the fit of docked substrates in enzymes.
Voronoi polyhedra have many uses beyond the analysis of protein structures. For instance, they have also been used in the analysis of liquid simulations and in weighting sequences to correct for over- or under-representation in an alignment. In non-biological applications, they are used in "nearest-neighbor" problems (trying to find the neighbor of a query point) and in finding the largest empty circle in a collection of points. The dual of a Voronoi diagram is a Delaunay triangulation. Since this triangulation has the "fattest" possible triangles, it is convenient for such procedures as finite element analysis. Furthermore, the border of Delaunay triangulation is the convex hull of an object, which is useful in graphics.
The simplest method for calculating volumes with Voronoi polyhedra is to put all atoms in the system on a grid. Then go to each grid-point (i.e. voxel) and add its volume to the atom center closest to it. This is prohibitively slow for a real protein structure, but it can be made somewhat faster by randomly sampling grid-points. It is, furthermore, a useful approach for high-dimensional integration and for the curved dividing surface approach discussed later.
More realistic approaches to calculating Voronoi volumes have two parts: (1) for each atom find the vertices of the polyhedron around it and (2) systematically collect these vertices to draw the polyhedron and calculate its volume.
In the basic Voronoi construction (Figure 7), each atom is surrounded by a unique limiting polyhedron such that all points within an atom’s polyhedron are closer to this atom than all other atoms. Points equidistant from two atoms are on a plane; those equidistant from three atoms are on a line, and those equidistant from four centers form a vertex. One can use this last fact to easily find all the vertices associated with an atom. With the coordinates of four atoms, it is straightforward to solve for possible vertex coordinates using the equation of a sphere.* One then checks whether this putative vertex is closer to these four atoms than any other atom; if so, it is a vertex.
In the procedure outlined above, all the atoms are considered equal, and the dividing planes are positioned midway between atoms (Figure 6). This method of partition, called bisection, is not physically reasonable for proteins, which have atoms of obviously different size (such as oxygen and sulfur). It chemically misallocates volume, giving an excess to the smaller atom.
Two principal methods of re-positioning the dividing plane have been proposed to make the partition more physically reasonable: method B and the radical-plane method. Both methods depend on the radii of the atoms in contact (R1 and R2) and the distance between the atoms (D).
Representing Motion Pathways as "Morph Movies"
One of the most interesting of the complex data types kept in the database are "morph movies" giving a plausible representation for the pathway of the motion. These movies can immediately give the viewer an idea of whether the motion is a rigid-body displacement or involves significant internal deformations (as in tomato bushy stunt virus versus citrate synthase). Pathway movies were pioneered by Vorhein et al., who used them to connect the many solved conformations of adenylate kinase.
Normal molecular-dynamics simulations (without special techniques, such as high temperature simulation or Brownian dynamics) cannot approach the timescales of the large-scale motions in the database. Consequently a pathway movie cannot be generated directly via molecular simulation. Rather, it is constructed as an interpolation between known endpoints (usually two crystal structures). The interpolation can be done in a number of ways.
Straight Cartesian interpolation. The difference in each atomic coordinate (between the known endpoint structures) is simply divided into a number of evenly spaced steps, and intermediate structures are generated for each step. This was the method used by Vorhein et al. It is easy to do, only requiring that the beginning and ending structures be intelligently positioned by fitting on a motionless core. However, it produces intermediates with clearly distorted geometry.
Interpolation with restraints. This is the above method where each intermediate structure is restrained to have correct stereochemistry and/or valid packing. One simple approach is to minimize the energy of each intermediate (with only selected energy terms) using a molecular mechanics program, such as X-PLOR. This technique will be described more fully in a forthcoming paper (Krebs & Gerstein, manuscript in preparation). The database, furthermore, is currently home to an experimental server that applies this interpolation technique to two arbitrary structures, generating a movie.
ANALYSIS OF Amino Acid Composition of Linker Sequences
Now that we have developed a database of protein motions, an essentially structure-orientated database, we want to use this to help interpret the mass of sequence data coming out of genome sequencing projects. In this way we are extrapolating ideas developed on the (relatively) smaller structure database to the much larger sequence database. We propose to do this through the calculation of two propensity scales for amino acids to be in linkers or flexible hinges.
Solved protein structures typically reveal different domains of proteins and linker regions between these domains. Linker regions are typically flexible, and, as such, form the basis for the hinge regions that allow two protein domains or fragments to move relative to each other as a part of a hinge mechanism.
Information about the amino acid composition of linker sequences can potentially be used to predict protein domains in protein sequences of unknown structure. In particular, a profile of flexible linker regions might be used to predict the location of domain hinges, for structural annotation of genome sequences.93 Here we present some preliminary results involving two methods for statistical analysis of linker sequences.
Propensities for Linkers in General
Our first method of analysis of linker sequences includes both flexible as well as inflexible linkers. In this method we have arbitrarily defined a linker sequence as the 16 residue region centered around the peptide bond linking two domains.
The analysis of the amino acid composition of linker sequences is an example of deriving sequence information from structural information. The structural information (i.e., the location of protein domains) can be found in the Structural Classification of Proteins (SCOP). SCOP contains several databases of amino acid sequences of protein domains. In our study, the PDB40 database provided by SCOP has been used to create a database of linker sequences. The PDB40 database comprises a subset of proteins in the Protein Data Bank (PDB) with known structure selected so that, when aligned, no two proteins in the subset show a sequence identity of 40% or greater. Thus, the data set is not biased towards protein structures listed multiple times in the PDB. We were able to extract 234 linker sequences from the PDB40 database, although the PDB40 database itself contains about 1,500 protein sequences. This mainly reflects the fact that many proteins consist of only a single domain and therefore contain no linker region.
Figure 8 compares the average amino acid composition of the linker sequences with the average amino acid composition of the PDB40 database, while Table 3 shows in more detail the profile of the amino acid composition at each of the sixteen positions in the linker sequence. For an interpretation of these results it is important to compute two-sided P-values to determine which amino acids show statistically different frequencies in linkers than in the database as a whole. (A two-sided P-value represents the probability that, in a data set of equal size drawn at random from the PDB40 database, a given amino acid would have a frequency of occurrence as different as or more different from its occurrence in the entire PDB40 database than what was actually observed in the linker subset.) Figure 9 shows the P-values for the average amino acid composition in the linkers. We are able to conclude, with better than 98% confidence, that linker regions are proline-rich and alanine- and trypthophan-poor. In particular, the statistical evidence that linkers are proline-rich is unusually strong and is significant at better than the hundredth-of-a-percent level. Table 4 shows the P-values of the amino acids at each of the sixteen linker positions.
In Table 4 and Figure 9 the amino acids have been roughly grouped according to the attributes hydrophobic, charged, and polar (following the classification of Branden and Tooze). As shown in Table 4 and Figure 9, the frequencies of the remaining amino acids in linkers are not statistically different from the database as a whole at the 5% significance level.
The statistical significance of the results of the computed amino acid averages can be assessed by comparing the composition of the linker sequences with random data sets of sequences of the same length and the same amount taken from the PDB40 database. The number of times a single amino acid occurs in multiple random data sets follows the binomial distribution according to the familiar equation:
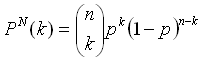
Here, p is the probability that the amino acid occurs in the PDB40 database, and Pn(k) is the probability that the amino acid occurs k times in a data set of n samples (n = 234 for the distribution of every single of the sixteen linker positions and n = 234 x 16 for the distribution of the linker average). The ratio k/n represents the fraction of the amino acid in the data set. Knowledge of the distribution functions of the amino acids then allows the calculation of P-values from the cumulative distribution function:
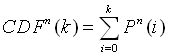
The value of CDFn(k) is the probability that the number of counts of an amino acid in a random data set would be less than k. Consequently, if o and e represent the observed and expected counts, then the two-sided P-value is given by 1-CDFn(e+|o-e|) + CDFn(e-|o-e|). This is simply the probability that the number of counts observed in a random subset of PDB40 would take on a value more different from what was expected than what was observed. In order to assign a P-value to an amino acid frequency in the linkers data set, the discrete values of the cumulative distribution function have been linearly interpolated. In most cases, it is also possible to obtain a satisfactory approximation to the P-values by applying the two-sided significance test to the Normal approximation of the Binomial distribution.
Towards Propensities for Flexible Linkers
A variant on this procedure involves focusing just on linkers that are known to be flexible. Our Database of Macromolecular Motions contains residue selections for known protein hinge regions (i.e., flexible linkers) that have been culled from the scientific literature. These sequences have been verified manually to be true flexible linker regions, and thus this database constitutes a potential "gold standard" free from algorithmic biases that can be used as a starting point in the development of propensity scales and other research leading towards algorithmic techniques. By expanding these residue selections slightly with a predetermined protocol and extracting the corresponding sequences from the PDB, a series of sequences of known flexible linkers may be obtained. A FASTA search with a suitable cutoff (e.g., e-value 0.001) may then be performed on known linker sequence to obtain a series of near homologues (Table 6).These homologues can then be arranged into a multiple alignment (via the CLUSTALW) program and the multiple alignment can be fused into a variety of consensus pattern representations, such as Hidden Markov Models or simply consensus sequences. A sample multiple alignment for the hinge in calmodulin is shown in Table 6 and a number of consensus sequences are shown in Table 5. The amino acid composition may be averaged over all the different hinges and different positions within a hinge to give a single composition vector for flexible hinges. Finally, this can be compared to the overall amino acid composition or that of linkers to obtain a preliminary scale of amino acid propensity in mobile linkers, as shown in Table 7. This can be compared with the scale of amino acid propensities in linkers as obtained by the procedure previously described and shown in Table 3.
Conclusion and Future Directions
We have developed a number of database-based techniques for the study of macromolecular motions. We have constructed a database of macromolecular motions, which currently documents ~120 motions, and have developed a classification scheme for the database based on size then packing (whether or not there is motion across a well-packed interface). The database incorporates innovative cooperatively features, allowing authorized remote experts to act as database editors via the Internet. We also developed a standardized nomenclature, such as maximum atomic displacement or degrees of rotation. We are developing automated tools to analyze protein and nucleic acid structures and sequences with possible motions, to extract standardized statistics on macromolecular motions from structural data, and allow the database to be more readily populated.
We expect that the number of macromolecular motions will greatly increase in the future, making a database of motions somewhat increasingly valuable. Our reasoning behind this conjecture is as follows: The number of new structures continues to go up at a rapid rate (nearly exponential). However, the increase in the number of folds is much slower and is expected to level off much more in the future as the we find more and more of the limited number of folds in nature, estimated to be as low as 1000. Each new structure solved that has the same fold as one in the database represents a potential new motion -- i.e. it is often a structure in a different liganded state or a structurally perturbed homologue. Thus, as we find more and more of the finite number of folds, crystallography and NMR will increasingly provide information about the variability and mobility of a given fold, rather than identifying new folding patterns.
Databases potentially represent a new paradigm for scientific computing. In an (over-simplified!) cartoon view, scientific computing traditionally involved big calculations on fast computers. The aim in these often was prediction based on first principles -- e.g. prediction of protein folding based on molecular dynamics. These calculations naturally emphasized the processor speed of the computer. In contrast, the new "database paradigm" focuses on small, inter-connected information sources on many different computers. The aim is communication of scientific information and the discovering of unexpected relationships in the data – e.g. the finding that heat shock protein looks like hexokinase. In contrast to their more traditional counterparts, these calculations are more dependent on disk-storage and networking rather than raw CPU power.
Acknowledgements
The authors gratefully acknowledge the financial support of the National Science Foundation (Grant DBI-9723182) and the numerous people who have either contributed entries or information to the database or have given us feedback on what the user community wants. The authors also wish to thank Informix Software, Inc. for providing a grant of its database software.
All correspondence to Mark.Gerstein@yale.edu.
References